一、图像分类

1、数据驱动方法

用到两个函数，一个是训练函数，接受图片和标签，然后输出模型；另一个是预测函数，接收一个模型，对图片种类进行预测。 这种算法是在训练集中找到最相似的样本，从而给待识别的图片打上与样本一样的标签。

2、K最近邻算法（KNN）

在 KNN 算法中，当需要对新的输入数据进行分类或预测时，它会查找与新数据“最近”的训练数据点，然后根据这些邻居的信息来进行分类或预测。当K值越大，表示距离越远，涵盖到的元素越多，预测结果更准确。

3、线性分类

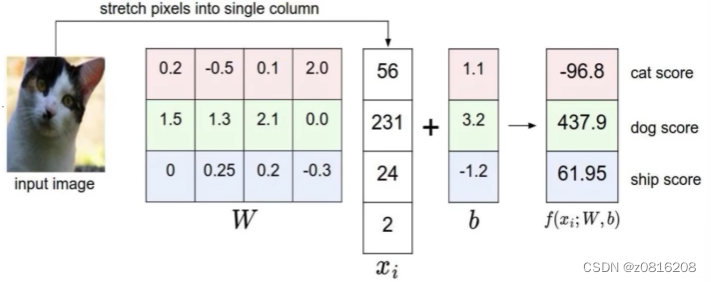
拿到一个图片数据（此处举例32*32像素的图片），将它拉伸为一个32*32*3的三维长向量，3代表3个颜色通道——红绿蓝。还存在一个参数矩阵W，把这个代表图片像素的列向量当作输入，转化成10个数字评分，这10个数字对应CIFAR-10数据里各个分类的得分。某一种分类的得分越高，那图片就更可能是这一类。

线性分类可以解释为每个种类的学习模板，对图片的每个像素和10个分类里的每一项，矩阵W里都有一些对应的项告诉我们该像素对该分类有多少影响。也就是说，矩阵W里的每一行都对应一个分类模板，如果我们解开这些行的值（成图片大小），那么每一行又分别对应一些权重，每个图像像素值和对应那个类别的一些权重，将这行分解回图像的大小，我们就可以可视化学到每个类的模板。

还有一种对线性分类器的解释是学习像素在高维空间的一个线性决策边界，其中高维空间就对应了图片能取到的像素密度值。

二、神经网络原理

1、输入层

在神经网络中，输入层是神经网络的第一层，负责接收外部输入数据并将数据传递给网络的隐藏层，而不需要对输入数据进行额外的处理。

输入层的神经元数量通常与输入数据的特征维度相对应，每个神经元对应输入数据的一个特征。 例如，如果输入数据是一个包含 100 个特征的向量，那么输入层将有 100 个神经元。

每个输入数据特征通过权重连接到输入层的神经元，神经元对输入数据进行加权求和，并应用激活函数后输出结果。

2、全连接层

在全连接层中，每个神经元与上一层的所有神经元相连接，每个连接都有一个对应的权重，这样每个神经元的输出是上一层所有神经元的加权和，再加上一个偏置值。

全连接层的参数量大、表达能力强，容易导致模型过拟合的问题，需要适当的正则化方法来缓解过拟合。

 3、前向传播

图片数据像素值x与权重W相乘可以得到一个得分值，再通过损失函数可以得到损失值

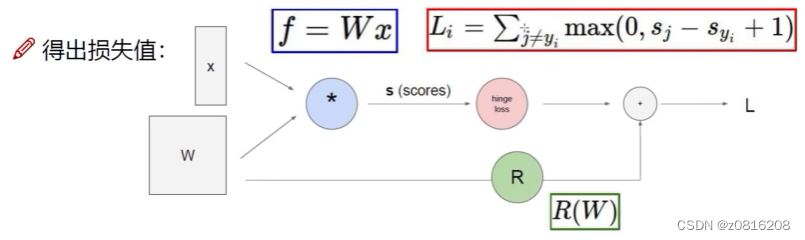
通过这些计算，我们最终还是得到一个得分值，但要进行图像分类，我们最终还是希望得到一个概率值，比如说输入一张猫猫图片，我们希望得到这张图片被计算机认定为是猫猫的概率是多少。

Softmax分类器 

我们可以通过下面的公式计算概率。

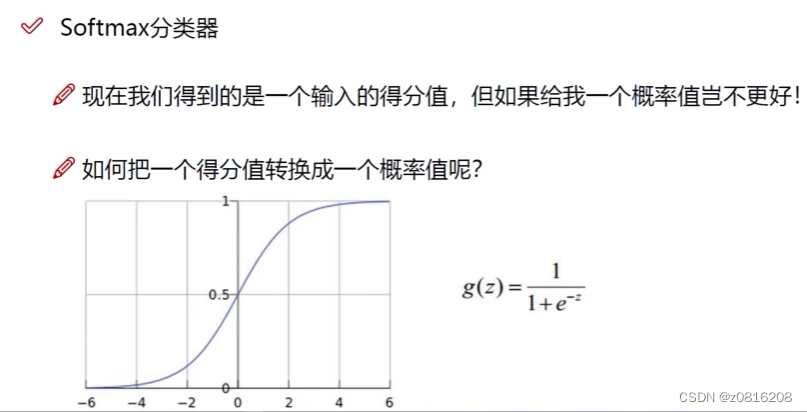
 在得到得分x后，可以通过指数函数e的x次方将x放大，更直观地看到不同得分x之间的差距，再计算该得分在所有得分中的占比，如果占比越大（越接近1），那么取负对数后就越接近0，即实际损失值越小。

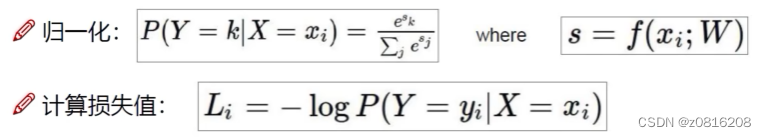
 4、激活函数

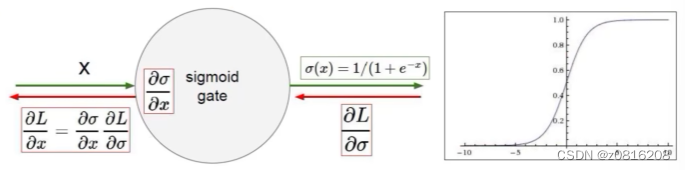
Sigmoid函数

将输入值映射到一个介于0和1之间的输出值。

当输入较大或较小时，Sigmoid函数的导数趋近于0，会引起导致梯度消失问题，这会影响深层神经网络的训练效果。

而且它的输出不以零为中心，这可能导致神经网络的后续层难以学习。

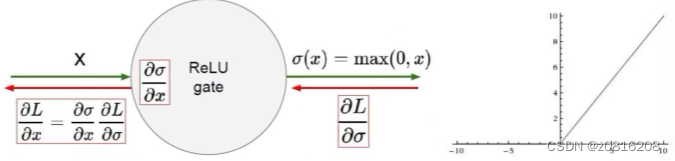
ReLU函数

将输入值映射为非负数，如果输入小于等于零，则输出为零；如果输入大于零，则输出与输入相等

如果ReLU函数的输入小于零，对应的神经元将永远不会被激活，导致这些神经元对于梯度的更新没有贡献，即神经元死亡问题。

ReLU函数在输入小于等于零时输出为零，这使得ReLU的输出不以零为中心，可能导致后续层的权重更新不平衡。

 5、损失函数和优化

损失函数（Loss Function）是用来衡量模型预测结果与真实标签之间差距的函数。损失函数通常在训练过程中被最小化，帮助模型不断调整参数以提高预测的准确性。

其中sj表示错误分类的得分，sy表示正确分类的得分。由此可知当正确分类的得分低于错误分类时，损失函数取到正值，反之取到0（毫无损失）

但若是不同的模型也会有损失函数的值相同的情况，这个时候我们不能认为两个模型一样，这里就需要引入正则化惩罚项，防止模型过拟合

6、反向传播（梯度下降）

在得到一个损失值L之后，如果这个L值不理想，则说明权重W值不合适，需要被优化。

从输出层到输入层，利用链式法则逐层计算损失函数对每个参数的梯度，更新优化参数，使得损失值最小。

 

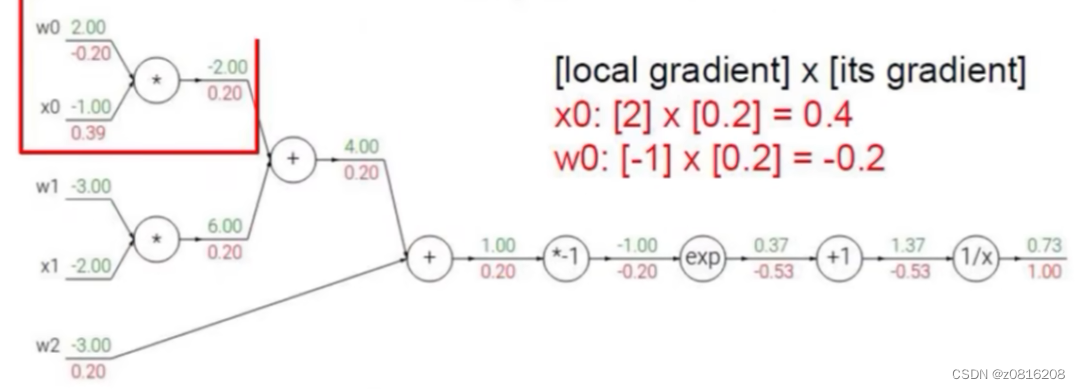
绿色代表输入值，红色代表梯度。以最后的0.73为例，从后往前传的梯度为1.00，而这一层本身的梯度是对1/x求导，再将1.37代入，得到这层本身梯度是-0.53，将后一层传过来的梯度乘以这一层本身的梯度，即为前一层的梯度。

前向传播与反向传播不断循环，最终可使梯度下降，优化参数，达到损失值下降的效果。

7、解决过拟合的办法

DROP-OUT正则化技术

在训练阶段，以一定的概率（通常为0.5）丢弃部分神经元，也就是说这些神经元不参与前向传播和反向传播的计算，从而减少模型对特定神经元的依赖性，增强模型泛化能力。

在测试阶段，所有神经元都参与前向传播和反向传播的计算，但其输出值需要按照训练阶段的概率进行缩放，以保持期望的输出值。