优化函数

经验风险最小化

这是一种比较常见的方法，将最小化风险变成了一个可以被优化算法解决的优化问题，经验风险函数为：
$${\mathbb{E}}_{x,y\sim p_{data}}[L(f(x;\theta ),y]=\frac{1}{m}\sum _{i=1}^{m}L(f(x^{(i)};\theta ),y^{(i)})$$
但是，这种方式很容易过拟合。

代理损失函数

代理损失函数使原函数的替代形式，如01损失转换成负对数等。相较于之前的优化函数，他能从样本集里抽取到更多信息。

批量算法和小批量算法

使用整个训练集优化的算法被称为批量或确定性梯度算法。
使用单个样本优化的算法被称为随机或在线算法。
大多数深度学习算法介于二者之间，选择小批量进行优化。

• 更大的批量会计算更精确的梯度估计，但回报小
• 极小的批量无法充分利用多核架构
• 在某些硬件上使用2的幂次的批量大小可以获得更少的运行时间
• 小批量学习时可能是由于加入了噪声，会产生一些正则化效果。泛化误差在批量大小为1时最好

神经网络优化中的挑战

• 病态
  见深度学习-1.数值计算
• 局部极小值
  在低维空间中非凸函数很可能会出现一些局部极小值点，较为常见。
• 高原、鞍点和其他平坦地区
  在高维空间中很少出现局部极小值点，鞍点却经常出现。此时无法使用牛顿法，而无鞍牛顿法应运而生。
• 悬崖和梯度爆炸
  多层神经网络通常存在像悬崖一样的斜率较大的区域，遇到这种情况时可以使用梯度截断的方式。
• 长期依赖
  神经网络学习新的样本特征时把旧的特征遗忘了。例如RNN中需要经常使用相同的权重矩阵$W^t$，假设该矩阵能够进行特征值分解，则$W^t=Vdiag(\lambda {)}^t{V}^{-1}$，显然当t增大时，特征值累乘会发生梯度爆炸和梯度消失的问题
• 非精确梯度
  当目标函数难以计算梯度时，或目标函数不可解时，只能对梯度进行近似。
• 局部和全局结构的弱对应
  例如优化函数没有局部极小值点，最小值只能在边界上寻找到时：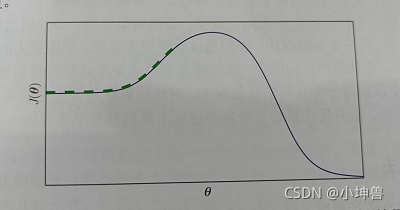
  随着梯度下降很有可能找不到右侧的最小值，而陷入了左侧的“最小值”
• 优化的理论限制
  一些研究表明，任何一种深度学习优化算法都有性能上的限制。

基本算法

随机梯度下降

Require:学习率r，初始参数theta

while 停止准则未满足：
	随机抽取batchsize个样本
	计算梯度g
	应用更新theta = theta - r * g

• 总结：最为常用的优化算法，重点在于选取学习率

动量

Require: 学习率r，动量参数alpha，初始参数theta，初始速度v

while 停止准则为满足：
	随机抽取batchsize个样本
	计算梯度g
	计算速度更新v = a * v - r * g
	应用更新theta = theta + v

• 总结：主要是为了解决病态问题

Nesterov动量

Require: 学习率r，动量参数alpha，初始参数theta，初始速度v

while 停止准则为满足：
	随机抽取batchsize个样本
	计算梯度g   ！！（关于theta + alpha * v）！！
	计算速度更新v = a * v - r * g
	应用更新theta = theta + v

• 总结：主要也是为了解决病态问题，在凸批量梯度的情况下收敛率从O(1/k)改进到了O(1/k^2)

参数初始化策略

• 标准初始化：$W_{i,j}\sim U(-\sqrt{\frac{6}{m+n}},\sqrt{\frac{6}{m+n}})$
• 随机正交初始化：初始化为随机正交矩阵
• 系数初始化：每个单元初始化为恰好有k个非零权重

自适应学习率算法

AdaGrad

• 对于偏导大的参数增大学习率，反之减小学习率

Require:全局学习率epsilon，初始参数theta，小常数delta
初始化梯度累积变量r = 0
while 没有达到停止准则:
	选取样本x -> y
	计算梯度g
	累积平方梯度 r += g * g
	应用更新 theta -= epsilon / (delta + sqrt(r)) * g

• 适用于凸优化问题，有令人满意的结果
• 从训练开始时积累梯度平方和会导致有效学习率过早和过量减小

RMSProp

• AdaGrad的改进，使其在非凸优化问题上效果变好，将梯度累计变成指数加权的移动平均

Require：全局学习率epsilon，衰减速率rho，初始参数theta，小常数delta
初始化累计变量r = 0
while 没有达到停止准则:
	选取样本x -> y
	计算梯度g
	累积平方梯度 r = rho * r + (1 - rho) * g * g
	应用更新 theta -= epsilon / (sqrt(delta + r)) * g # 逐元素计算

• 该算法已被证明是一种有效且实用的深度神经网络优化算法

Adam

• 另一种学习率自适应算法

Require：步长epsilon，矩估计衰减速率p1，p2（建议默认为0.9和0.99）
Require：初始参数theta，数值稳定用的小常数delta（建议默认为1e-8）
s, r = 0, 0  # 初始化一阶二阶矩变量 
t = 0  # 初始化时间步
while 没有达到停止准则:
	选取样本x -> y
	计算梯度g
	t += 1
	s = p1 * s + (1 - p1) * g  # 更新一阶有偏矩估计
	r = p2 * r + (1 - p2) * g * g  # 更新二阶有偏矩估计
	ss = s / (1 - p1 ^ t)  #修正一阶矩的偏差
	rr = r / (1 - p2 ^ t)  #修正二阶矩的偏差
	theta -= epsilon * ss / (sqrt(rr) + delta)

• 对超参数的选择相当鲁棒

二阶近似方法

牛顿法

每轮迭代参数$\theta$时，使用二阶海森矩阵迭代：
$$\theta =\theta -H^{-1}g$$
带牛顿法在鞍点附近（海森矩阵非正定）会失效，因此需要做一个正则化来近似
${\theta }^{\ast }={\theta }_0-[H(f({\theta }_0))+\alpha I{]}^{-1}{\nabla }_{\theta }f({\theta }_0)$

共轭梯度

由于梯度下降法会受到病态的海森矩阵的影响，导致收敛速度非常慢，因此采用共轭梯度下降，每次迭代的方向与想以此的方向共轭，则可以拜托这种病态的影响。

BFGS

该算法由牛顿法的一些优点，但没有其计算逆矩阵的负担。

优化策略和元算法

批标准化

他不是一个优化算法，而是一个自适应的重参数化方法，试图解决训练非常深的模型的困难。
对于非常深的神经网络，每一轮迭代时由于我们同时使用了同时更新所有参数的方式，可能会造成意想不到的情况。
例如对于神经网络
$$f(x)={\omega }_4{\omega }_3{\omega }_2{\omega }_{1}x$$
我们进行一步更新得到的新值是
$$f(x)=({\omega }_4-{ϵ}_4)({\omega }_3-{ϵ}_3)({\omega }_2-{ϵ}_2)({\omega }_1-{ϵ}_1)x$$
当某几项的系数较大时，很可能会出现梯度爆炸的问题。尤其当网络层数更深时尤为严重。
因此，批标准化提供李毅中几乎可以重参数化所有深度网络的优雅方法，显著见笑了多层之间协调更新的问题。
他可以应用在网络的任何输入层或隐藏层，设$H$是需要标准化的某层的小批量激活函数，排布为设计矩阵，每个样本的激活出现在矩阵的每一行中。为了标准化$H$，我们将其替换为$H^{\prime }=\frac{H-\mu }{\sigma }$，其中$\mu =\frac{1}{m}{\sum }_i{H}_{i,:}$，$\sigma =\sqrt{\delta +\frac{1}{m}{\sum }_i(H-\mu {)}_i^2}$，$\delta$是一个很小的正值，强制避免遇到梯度为零时产生的一些未定义的问题。

坐标下降

将优化问题分成几部分，每次只优化一个维度或几个维度。

Polyak平均

每次迭代时，会找到其所经过的点的平均。使用这种方法具有较强的收敛保证。