本分类专栏博客系列是学习《深入浅出强化学习原理入门》的学习总结。
书籍链接：链接：https://pan.baidu.com/s/1p0qQ68pzTb7_GK4Brcm4sw 提取码：opjy

基于TRPO的强化学习方法

TRPO 是英⽂单词 Trust Region Policy Optimization 的简称，翻译成中⽂是 置信域策略优。

在TRPO出来之前，⼤部分强化学习算法很难保证单调收敛，⽽TRPO却给出了⼀个单调的策略改善⽅法。所以，不管你从事什么⾏业，如果想⽤强化学习解决问题，TRPO都是⼀个不错的选择。所以本章确实很关键。

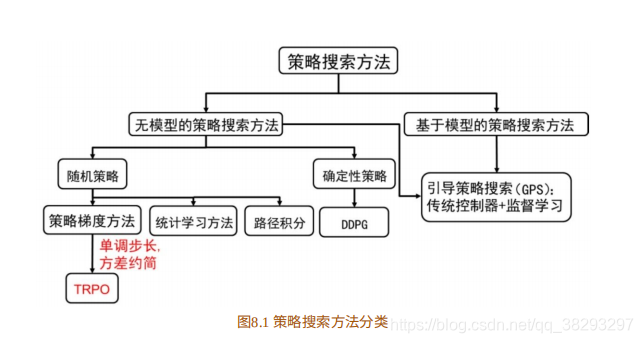
如图8.1所⽰为直接策略搜索⽅法的分类，根据模型是否已知，策略搜索⽅法分为⽆模型的策略搜索⽅法和基于模型的策略搜索⽅法。

• 在⽆模型的策略搜索⽅法中，根据策略是否随机可以分为随机策略搜索⽅法和确定 性策略搜索⽅法。在随机策略搜索⽅法中最先发展起来的是策略梯度的⽅法。然⽽，策略梯度⽅法最⼤的问题是步⻓的选取问题，若步⻓太⻓，策略很容易发散；若步⻓太短，收敛速度很慢。为了避免步⻓问题，学者们提出基于统计学习的策略搜索⽅法和基于路径积分的策略搜索⽅法。虽然这些⽅法能在⼀定程度上避免直接利⽤步⻓，但这些⽅法也丢掉了梯度⽅法很容易⽤来处理⼤规模问题的优势。TRPO没有选择回避更新步⻓的问题，⽽是正⾯解决这个问题。本章会循序介绍TRPO⽅法。

一、理论基础

根据策略梯度⽅法，参数更新⽅程式为：${\theta }_{new}={\theta }_{old}+\alpha {\nabla }_{\theta }J$

策略梯度算法的硬伤就在更新步⻓，当步⻓不合适时，更新的参数所 对应的策略是⼀个更不好的策略，当利⽤这个更不好的策略采样学习时， 再次更新的参数会更差，因此很容易导致越学越差，最后崩溃。所以，合适的步⻓对于强化学习⾮常关键。

什么才是合适的步⻓？

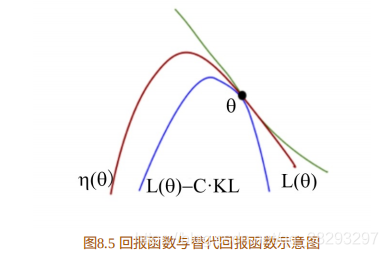
合适的步⻓是指当策略更新后，回报函数的值不能更差。那么如何选 择步⻓？或者说，如何找到新的策略使新的回报函数的值单调增⻓，或单调不减？这就是TRPO要解决的问题。

用 $\tau$ 表⽰⼀组状态-⾏为序列 $s_0,u_0,...,s_H,u_H$，强化学习的回报函数为：

上⽂已提及，TRPO是要找到新的策略使回报函数单调不减。⼀个⾃ 然的想法是能否将新的策略所对应的回报函数分解成旧的策略所对应的回报函数加其他项。这样，只要新的策略所对应的其他项⼤于等于零，那么 新的策略就能保证回报函数单调不减。TRPO的起点便是这样⼀个等式：

这⾥我们⽤ $\pi$ 表⽰旧的策略，⽤ $\tilde{\pi }$ 表⽰新的策略。其中
上式是优势函数。

此处我们再花点笔墨介绍下 $Q_{\pi }(s,a)-V_{\pi }(s)$ 为什么会被称为优势函数，这个优势到底是指和谁相⽐的优势？我们以⼤家熟悉的树状图来阐 述，如图8.2所⽰。

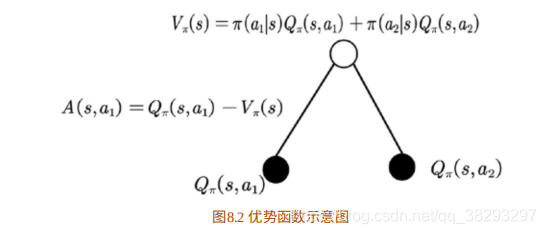
图8.2中的值函数 $V(s)$ 可以理解为在该状态 $s$下所有可能动作所对应的动作值函数乘以采取该动作的概率的和。通俗的说法是，值函数 $V(s)$ 是该状态下所有动作值函数关于动作概率的平均值。⽽动作值函数 $Q(s,a)$ 是单个动作所对应的值函数。 $Q_{\pi }(s,a)-V_{\pi }(s)$ 能评价当前动作值函数相 对于平均值的⼤⼩。所以，这⾥的优势指的是动作值函数相⽐于当前状态 的值函数的优势。如果优势函数⼤于零，则说明该动作⽐平均动作好，如 果优势函数⼩于零，则说明当前动作不如平均动作好。

回到正题上来，我们下⾯给出公式（8.2）的证明。

为了在等式（8.2）中出现策略项，我们需要对公式（8.2）进⼀步加⼯ 转化。如图8.3所⽰，我们对新旧策略回报差进⾏转化。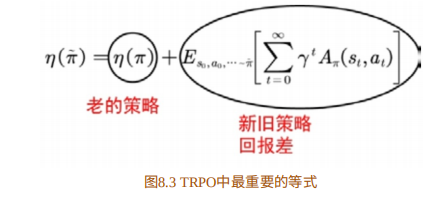




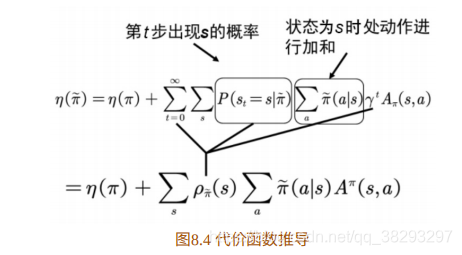
注意：这时状态 $s$ 的分布由新的策略 $\tilde{\pi }$ 产⽣，对新的策略严重依赖。

TRPO算法在推导过程中运⽤了四个技巧，我们分别阐述。