摘要： 上一节的压缩映射在实际迭代时可以分成两种方法，分别称作值迭代和策略迭代。本文用走迷宫的例子（将1维迷宫扩展到2维）讲这两种迭代。对应第一节参考链接[2]的前4章。

拆分压缩映射

  上一节的压缩映射 $v=f(v)$，展开写就是
$$\begin{array}{rl}v(s)=& \underset{\pi }{\max }\sum _a\pi (a|s)q(s,a)\\ =& \underset{a}{\max }q(s,a)\\ =& \underset{a}{\max }[r(s,a)+\gamma v(s^{\prime })]\\ =& \max [r(s,L)+\gamma v(s_L),r(s,R)+\gamma v(s_R)]\end{array}$$
中实际上每次迭代都隐含了两步，这两步按执行的先后顺序分为值迭代和策略迭代，之前例子是值迭代，因为过于简单看不出区别（一步迭代就找到了最优策略），这次换个复杂的例子。这个式子中的 $v(s_L)$ 和 $v(s_R)$ 分别表示当前状态左右两侧状态的价值函数，与策略有关，但策略又与状态价值函数有关，所以按照先更新价值函数还是先更新策略的不同分为两种迭代方法，值迭代和策略迭代。
  值迭代 指先找出使 $q(s,a)$ 最大时的 $\pi$，再迭代一步 $v=f(v)$ 称作值迭代。走迷宫时，$q(s,a)$ 建立成一个Q表，每次迭代中，找出表中Q值最大的动作作为 $f(v)$，然后求 $v=f(v)$。
  策略迭代 与值迭代相反，先迭代一步 $v=f(v)$，再找出使 $q(s,a)$ 最大时的 $\pi$，称作策略迭代。
  这里有个问题，使 $q(s,a)$ 最大时的 $\pi$ 应该是个定值，那么如果最优策略 $\pi$ 是个随机变量，是不是就迭代不到最优策略？

走迷宫的例子

  每个格子处有右上左下和不动5种状态，一开始的策略是每个状态都保持不动。策略编号0~5分别表示不动和右上左下。下图的迷宫中有一个终点和多个陷阱，回合奖励分别为$1$和$-10$。目标为从左上角出发走到终点。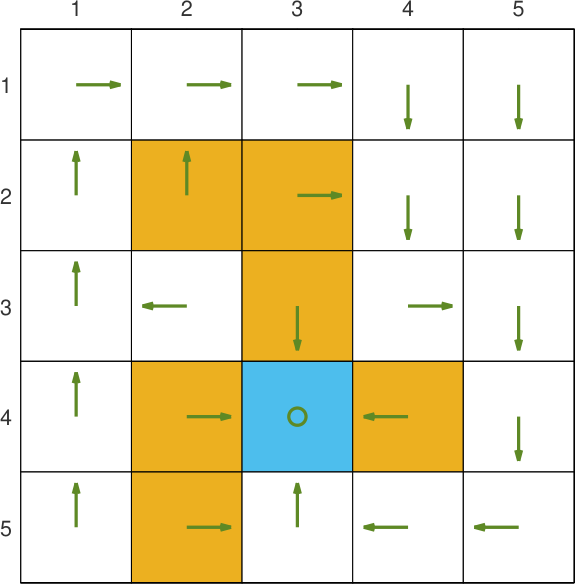

策略迭代

收敛后每个格子的状态价值函数如下图所示。

收敛后每个格子的策略如下图所示。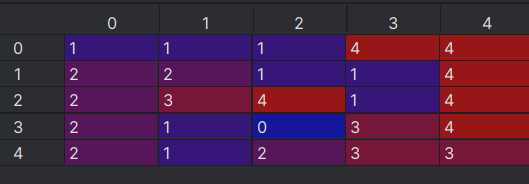

值迭代

附代码

策略迭代

import numpy as np

strategy = np.zeros([5, 5], dtype=int)
gamma = 0.8
MAZE_TRAP = [(1, 1), (1, 2), (2, 2), (3, 1), (3, 3), (4, 1)]  # 陷阱
MAZE_TERM = (3, 2)  # 终点

# 找出一个数组中的最大值索引，如果有多个最大值，就从中随机取一个
def Argmax_Rand(x: list) -> int:
    bestv = -1e12
    samevaluei = np.zeros(len(x), dtype=int)
    samecnt = 0
    for n in range(len(x)):
        if x[n] < bestv:
            continue
        elif x[n] > bestv:
            bestv = x[n]
            samecnt = 0
        samevaluei[samecnt] = n
        samecnt += 1
    return samevaluei[np.random.randint(samecnt)]

# 返回与一个网格`grid`相邻的第`adjacent`处方位的网格
def Find_Adjacent(grid: tuple, adjacent: int) -> tuple:
    ans = list(grid)
    if adjacent == 1:
        ans[1] += 1
    elif adjacent == 2:
        ans[0] -= 1
    elif adjacent == 3:
        ans[1] -= 1
    elif adjacent == 4:
        ans[0] += 1
    ans[0] = 0 if ans[0] < 0 else ans[0]
    ans[0] = 4 if ans[0] > 4 else ans[0]
    ans[1] = 0 if ans[1] < 0 else ans[1]
    ans[1] = 4 if ans[1] > 4 else ans[1]
    return tuple(ans)

# 迭代函数
def fx(x):
    y = np.zeros([5, 5])
    for m in range(5):  # 行
        for n in range(5):  # 列
            adjacent = Find_Adjacent((m, n), strategy[m, n])
            actionValue = gamma * x[adjacent]
            if adjacent in MAZE_TRAP:
                actionValue += -10
            elif adjacent == MAZE_TERM:
                actionValue += 1
            y[m, n] = actionValue
    return y

# 对每个格子进行策略改善
# grid: 当前格子
# value: 当前策略下的价值函数矩阵
# return: 当前格子的新策略
def Policy_Imporvement(grid: tuple, value):
    actionValues = []
    for m in range(5):  # 5个策略
        adjacent = Find_Adjacent(grid, m)
        actionValue = gamma * value[adjacent]
        if adjacent in MAZE_TRAP:
            actionValue += -10
        elif adjacent == MAZE_TERM:
            actionValue += 1
        actionValues.append(actionValue)
    return Argmax_Rand(actionValues)

# 主函数
vold = np.zeros([5, 5])
cntPolicyIter = 0
cntValueIters = []
while 1:
    # 策略评估（policy evaluation, PE）
    cntValueIter = 0
    while 1:
        vnew = fx(vold)
        err = sum(sum(vnew - vold))**2
        if err < 1e-6:  # 状态价值函数收敛时退出
            break
        vold = vnew
        cntValueIter += 1  # 策略评估的迭代步数
    pass
    # 策略改善（policy improvement, PI）
    strategyOld = strategy.copy()
    for m in range(5):  # 行
        for n in range(5):  # 列
            strategy[m, n] = Policy_Imporvement((m, n), vnew)  # 更新策略
    err = sum(sum(strategyOld - strategy))**2
    if err < 1e-6:  # 策略收敛时退出
        break
    cntPolicyIter += 1
    cntValueIters.append(cntValueIter)
print(cntPolicyIter)
print(cntValueIters)