第三章 神经网络

上一章我们学习了感知机，了解了其如何执行简单的逻辑运算，并发现它的局限性（如无法实现异或运算）。本章我们将从感知机自然过渡到更强大的神经网络模型，逐步建立起能执行复杂任务（如图像识别）的多层神经网络。

3.1 从感知机到神经网络

3.1.1 神经网络的示例

神经网络是一种由多个神经元（也称为节点或单元）构成的结构。它通过模拟人脑神经元的连接方式，将简单的单元组合成强大的信息处理系统。

以下图为例，一个典型的三层神经网络结构：

• 输入层：接收输入数据（如图像像素）

• 隐藏层：对输入进行特征提取

• 输出层：输出分类结果或数值预

3.1.2 复习感知机

感知机的公式是：

但这个“阶跃函数”不连续，难以用于梯度下降，因此我们引入激活函数。

3.1.3 激活函数登场

激活函数决定神经元的“激活程度”，让模型拥有非线性拟合能力，这样就可以解决异或问题，也使神经网络具备表示复杂函数的能力。

3.2 激活函数

3.2.1 阶跃函数的实现

def step_function(x):
    return np.array(x > 0, dtype=np.int32)

3.2.2 阶跃函数的图形

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.title("Step Function")
plt.show()

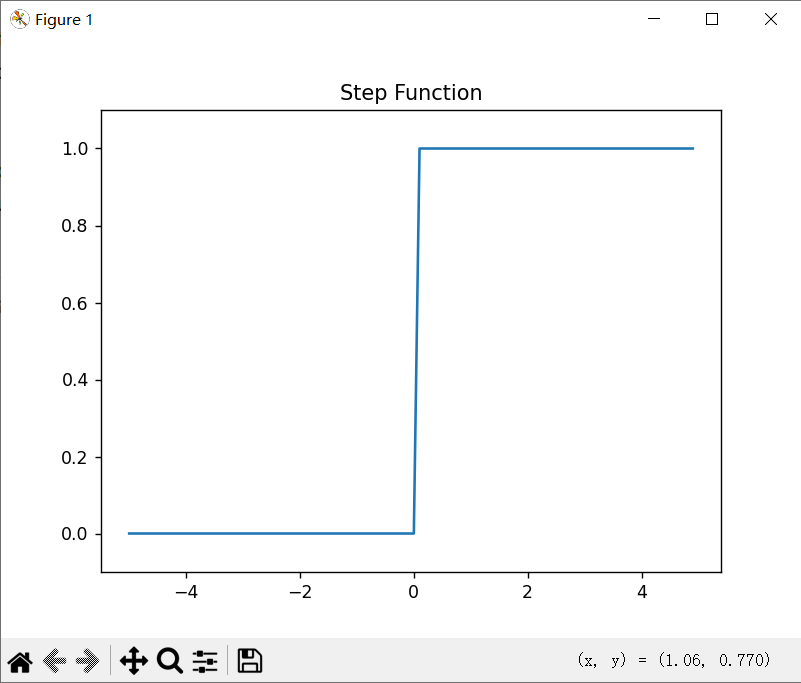
3.2.3 sigmoid函数

Sigmoid 是最常见的激活函数之一，其公式为：

其输出范围是 (0, 1)，适用于二分类问题。

3.2.4 sigmoid函数的实现

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

以下为sigmoid函数在相同区间的图像展示： 

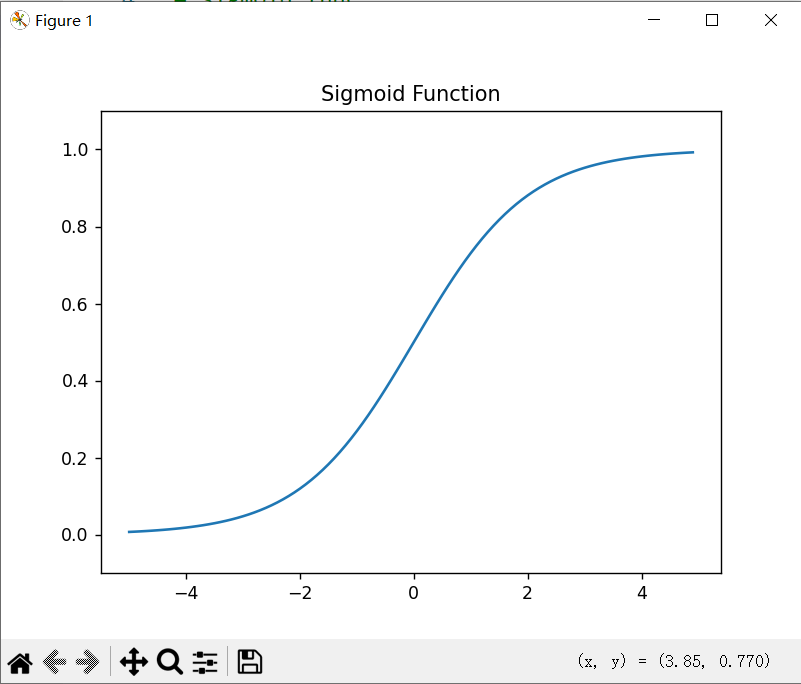
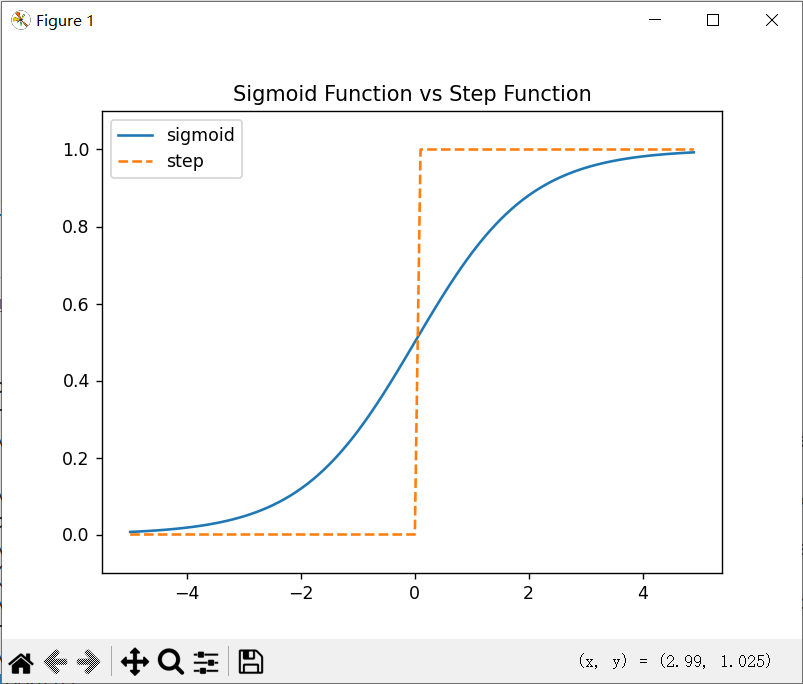
3.2.5 sigmoid函数和阶跃函数的比较

• 阶跃函数：输出只有 0 或 1，非连续，不能反向传播

• Sigmoid：输出0到1的连续区间，连续可导，可用于训练神经网络

3.2.6 ReLU函数

ReLU（Rectified Linear Unit）是当前最常用的激活函数：

def relu(x):
    return np.maximum(0, x)

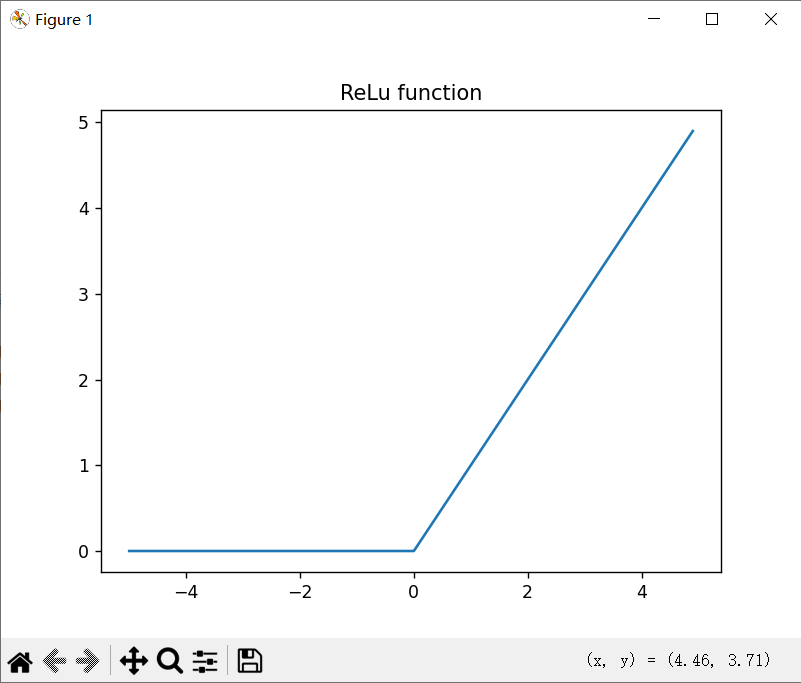
在现代深度学习中，ReLU等激活函数已逐渐取代Sigmoid在隐藏层的应用，但在输出层需要概率预测时，Sigmoid仍被广泛使用。阶跃函数则因其局限性，多出现在教学示例或特定应用场景中。

3.3 多维数组的运算

神经网络本质上是矩阵的乘法和加法组合，理解多维数组的运算非常关键。

3.3.1 多维数组

NumPy 中的多维数组可表示任意维度的数据：

    x = np.array([1,2,3,4],dtype=np.float16)
    print(np.ndim(x))   #   1
    print(x.shape)      #   (4,)
    x = np.array([[1,2],[3,4]],dtype=np.float16)
    print(np.ndim(x))   #   2
    print(x.shape)      #   (2,2)

注意：即使是一维，输出也是元组，而不是单个数字！ 

3.3.2 矩阵乘法

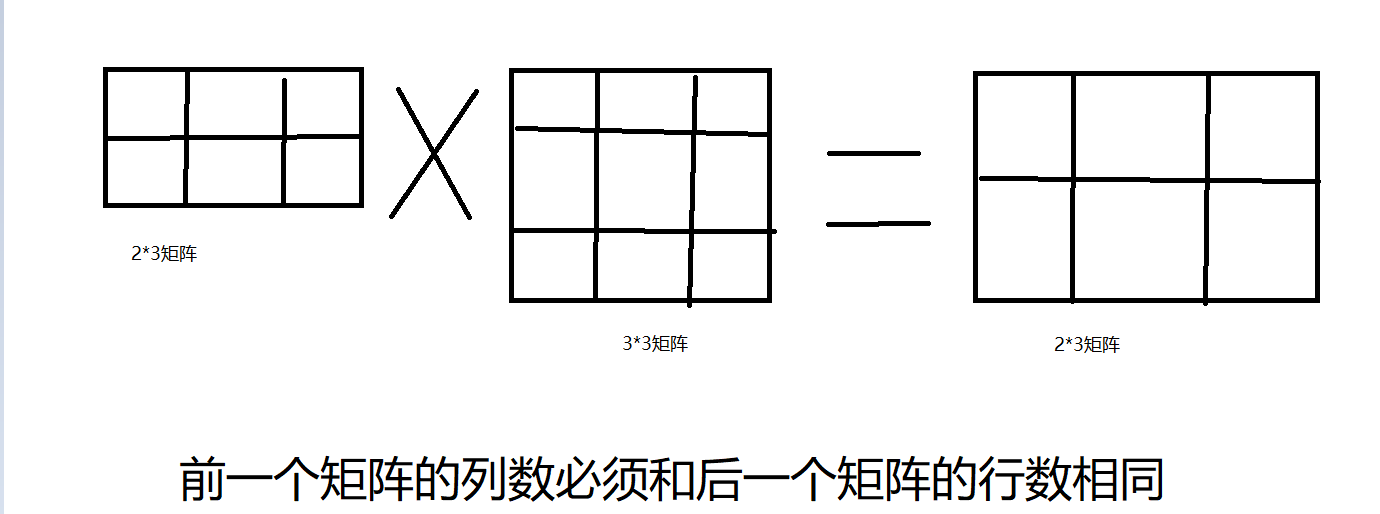
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
np.dot(A, B)

dot() 函数用于执行矩阵乘法，神经网络的前向传播通过矩阵乘法实现。例如，输入向量X与权重矩阵W相乘，加上偏置后通过激活函数：
A=XW+B
Z=σ(A)

神经网络第一层的输出计算示例（激活函数可替换其他）：

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)

3.4 三层神经网络的实现

3.4.1 符号确认

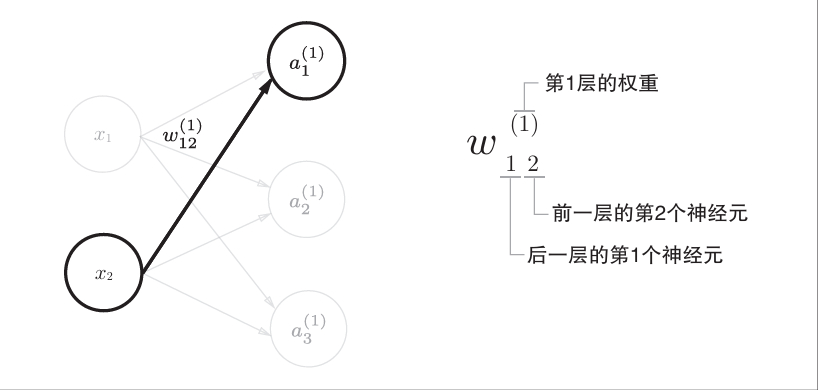
其他符号诸如“a”（输入加权和）,“z”（激活函数输出）同以上相似。

3.4.2 各层间信号传递的实现

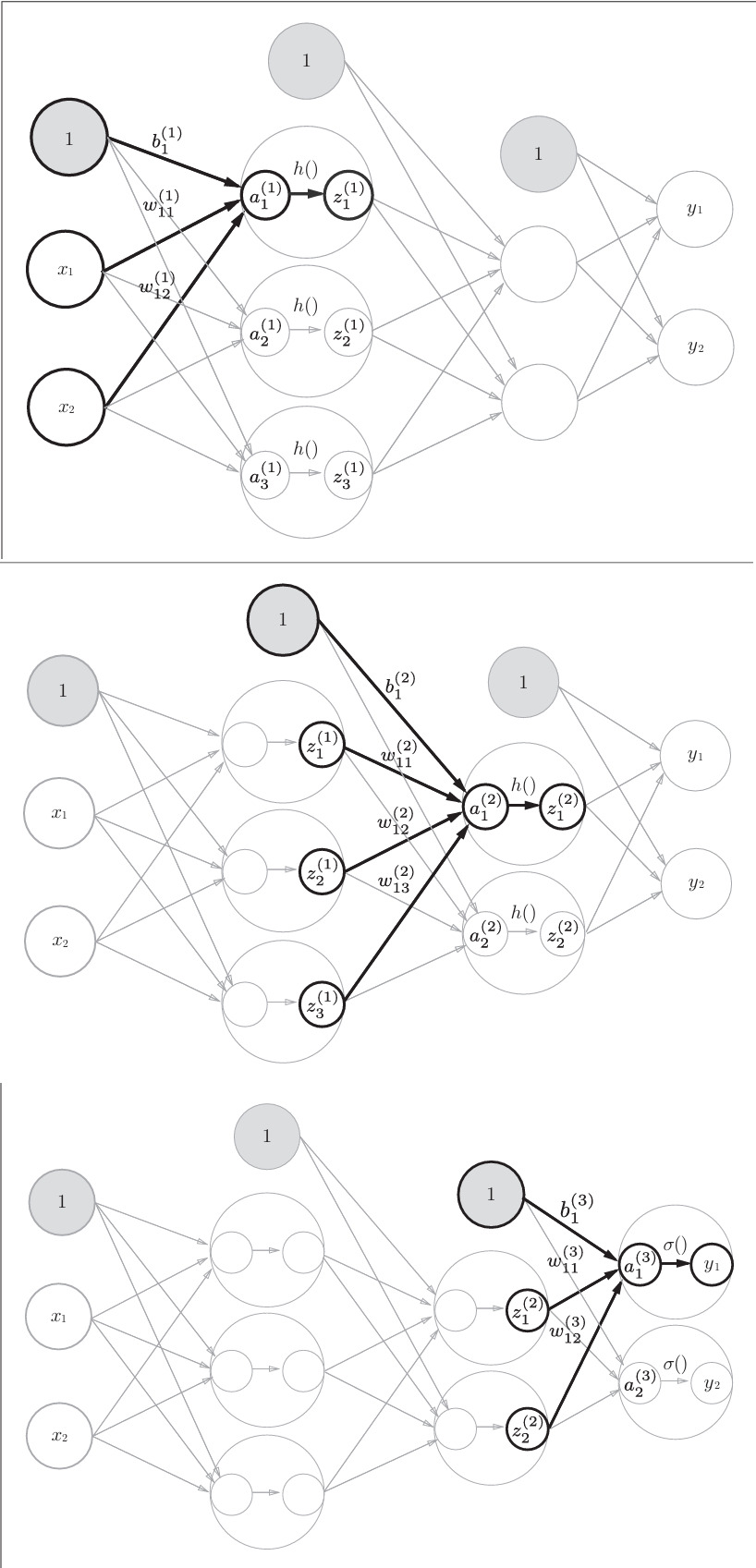
以上图像具体诠释了神经网络中各个信号间的传播流程。以下为代码部分：

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = a3  # 输出层使用恒等函数
    return y

神经网络就是“矩阵 + 激活函数”的组合，每一层都重复相同的流程。

3.5 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出 层的激活函数。一般而言，回归问题用恒等函数，分类问题用softmax函数。

📌 机器学习的问题大致可以分为分类问题和回归问题。分类问题是数 据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性 的问题就是分类问题。而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就 是回归问题（类似“57.4kg”这样的预测）。

3.5.1 恒等函数和 softmax 函数

恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直 接输出。因此，在输出层使用恒等函数时，输入信号会原封不动地被输出，恒等函数进行的转换处理可以用一根箭头来表示。

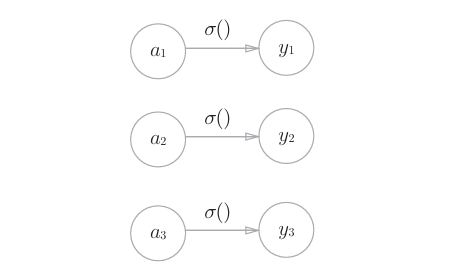
def identity_function(x):
    return x

分类任务使用 softmax：

用图表示softmax函数的话，softmax函数的输出通过箭头与所有的输入信号相连。

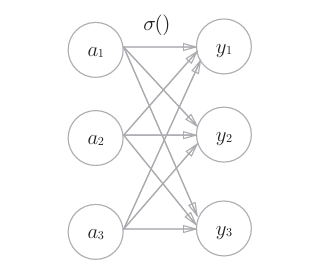
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

我们自己实现时要注意避免数值溢出，要减去最大值 c = np.max(a)。softmax函数的输出是0.0到1.0之间的实数。并且，softmax 函数的输出值的总和是1。输出总和为1是softmax函数的一个重要性质。正 因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。

一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果。 并且，即便使用softmax函数，输出值最大的神经元的位置也不会变（这是因为指数函数（y=exp(x)）是单调递增函数）。因此， 神经网络在进行分类时，输出层的softmax函数可以省略。在实际的问题中， 由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数 一般会被省略。

📌求解机器学习问题的步骤可以分为“学习”和“推理”两个阶段。首先，在学习阶段进行模型的学习，然后，在推理阶段，用学习完成的模型对未知的数据进行推理（分类）。如前所述，推理阶段一般会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关系（详细内容请参考下一章）

3.5.2 输出层的神经元数量

输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量。比如，对于某个输入图像，预测是图中的数字0到9中的哪一个的问题（10类别分类问题），可以像下图这样， 将输出层的神经元设定为10个。

3.6 手写数字识别

介绍完神经网络的结构之后，现在我们来试着解决实际问题。这里我们 来进行手写数字图像的分类。假设网络学习已经全部结束，我们使用学习到的参数，先实现神经网络的“推理处理”。这个推理处理也称为神经网络的前向传播（forward propagation）。

3.6.1 MNIST 数据集

这里使用的数据集是MNIST手写数字图像集。MNIST是机器学习领域 最有名的数据集之一，被应用于从简单的实验到发表的论文研究等各种场合。 实际上，在阅读图像识别或机器学习的论文时，MNIST数据集经常作为实 验用的数据出现。 MNIST数据集是由0到9的数字图像构成的（图3-24）。训练图像有6万张， 测试图像有1万张，这些图像可以用于学习和推理。MNIST数据集的一般 使用方法是，先用训练图像进行学习，再用学习到的模型度量能在多大程度 上对测试图像进行正确的分类。mnist数据集图像如下：

MNIST的图像数据是28像素 ×28像素的灰度图像（1通道），各个像素 的取值在0到255之间。每个图像数据都相应地标有“7”“ 2”“ 1”等标签。 

🎈虽然可以通过使用pytorch，TensorFlow这些框架来快速使用这个数据集，但是这样就违背我们这个系列初心了，而且读者以后总会遇见使用源数据集进行工作的情况，所以这里推荐大家去网站下载源数据集，这里贴一下kaggle的数据集链接：Digit Recognizer | KaggleLearn computer vision fundamentals with the famous MNIST datahttps://www.kaggle.com/c/digit-recognizer/data

这里给读者提供了基础可视化代码：

import numpy as np
import matplotlib.pyplot as plt

# 读取 CSV 文件（跳过表头）
def load_mnist_csv(path, num_images=5):
    data = np.loadtxt(path, delimiter=',', skiprows=1)
    labels = data[:num_images, 0].astype(int)
    images = data[:num_images, 1:].astype(np.uint8).reshape((-1, 28, 28))
    return images, labels

# 显示图像
def show_images(images, labels):
    plt.figure(figsize=(10, 2))
    for i in range(len(images)):
        plt.subplot(1, len(images), i + 1)
        plt.imshow(images[i], cmap='gray')
        plt.title(f"Label: {labels[i]}")
        plt.axis('off')
    plt.tight_layout()
    plt.show()

# 示例用法
if __name__ == "__main__":
    images, labels = load_mnist_csv('digit-recognizer/train.csv', num_images=5)
    show_images(images, labels)

 效果如下：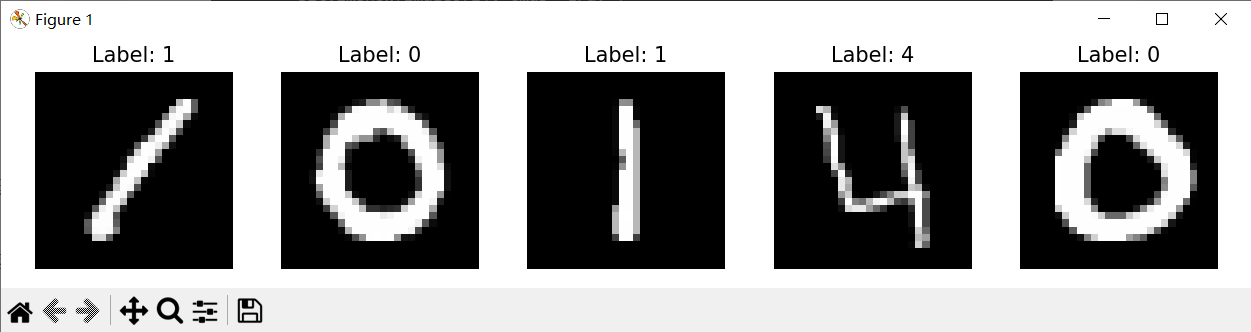

3.6.2 神经网络的推理处理

下面，我们对这个MNIST数据集实现神经网络的推理处理。神经网络 的输入层有784个神经元，输出层有10个神经元。输入层的784这个数字来 源于图像大小的28×28=784，输出层的10这个数字来源于10类别分类（数 字0到9，共10类别）。此外，这个神经网络有2个隐藏层，第1个隐藏层有 50个神经元，第2个隐藏层有100个神经元。这个50和100可以设置为任何值。实现代码如下（因为测试集没有label标签，所以这里挑选了train中若干图像来进行推理）：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def init_network():
    network = {}
    network['W1'] = np.random.randn(784, 50) * 0.01
    network['b1'] = np.zeros(50)
    network['W2'] = np.random.randn(50, 100) * 0.01
    network['b2'] = np.zeros(100)
    network['W3'] = np.random.randn(100, 10) * 0.01
    network['b3'] = np.zeros(10)
    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    return a3

def load_mnist_train_csv(path, max_samples=100):
    data = np.loadtxt(path, delimiter=',', skiprows=1)
    labels = data[:max_samples, 0].astype(int)
    images = data[:max_samples, 1:] / 255.0  # 归一化
    return images, labels

if __name__ == "__main__":
    images, labels = load_mnist_train_csv("digit-recognizer/train.csv", max_samples=1000)
    network = init_network()

    correct = 0
    for x, label in zip(images, labels):
        y = forward(network, x)
        pred = np.argmax(y)
        if pred == label:
            correct += 1

    accuracy = correct / len(images)
    print(f"Accuracy: {accuracy:.4f}")

使用网络对输入图片进行推理，输出预测的数字。

执行上面的代码后，会显示“Accuracy:0.09352”。这表示有9.352%的数据被正确分类了（完全盲猜的效果）。目前我们的目标是运行学习到的神经网络，所以不讨论识别精度本身，不过以后我们会花精力在神经网络的结构和学习方法上，思考如何进一步提高这个精度到95%以上。

将图像的各个像 素值除以255，使得数据的值在0.0～1.0的范围内。像这样把数据限定到某 个范围内的处理称为正规化（normalization）。此外，对神经网络的输入数据 进行某种既定的转换称为预处理（pre-processing）。这里，作为对输入图像的 一种预处理，我们进行了正规化。

🎆预处理在神经网络（深度学习）中非常实用，其有效性已在提高识别 性能和学习的效率等众多实验中得到证明。在刚才的例子中，作为 一种预处理，我们将各个像素值除以255，进行了简单的正规化。 实际上，很多预处理都会考虑到数据的整体分布。比如，利用数据 整体的均值或标准差，移动数据，使数据整体以0为中心分布，或 者进行正规化，把数据的延展控制在一定范围内。除此之外，还有 将数据整体的分布形状均匀化的方法，即数据白化（whitening）等。

3.6.3 批处理

以上就是处理MNIST数据集的神经网络的实现，现在我们来关注输入 数据和权重参数的“形状”。从整体的处理流程来看，输入一个由784个元素（原本是一 个28×28的二维数组）构成的一维数组后，输出一个有10个元素的一维数组。 这是只输入一张图像数据时的处理流程。

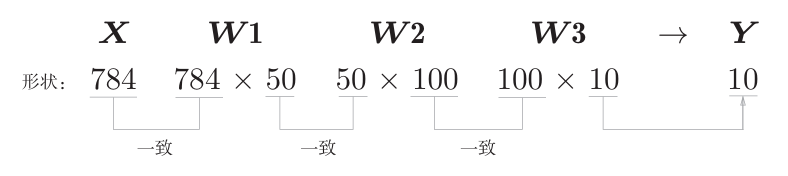
现在我们来考虑打包输入多张图像的情形。比如，我们想用predict() 函数一次性打包处理100张图像。为此，可以把x的形状改为100×784，将 100张图像打包作为输入数据。用图表示的话，如下所示。

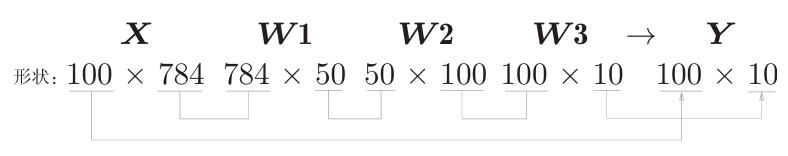
输入数据的形状为100×784，输出数据的形状为 100 ×10。这表示输入的100张图像的结果被一次性输出了。 这种打包式的输入数据称为批（batch）。批有“捆”的意思，图像就如同纸币一样扎成一捆。

🧨批处理对计算机的运算大有利处，可以大幅缩短每张图像的处理时 间。那么为什么批处理可以缩短处理时间呢？这是因为大多数处理 数值计算的库都进行了能够高效处理大型数组运算的最优化。并且， 在神经网络的运算中，当数据传送成为瓶颈时，批处理可以减轻数 据总线的负荷（严格地讲，相对于数据读入，可以将更多的时间用在 计算上）。也就是说，批处理一次性计算大型数组要比分开逐步计算 各个小型数组速度更快。

批处理修改代码如下： 

if __name__ == "__main__":
    images, labels = load_mnist_train_csv("digit-recognizer/train.csv", max_samples=1000)
    network = init_network()

    batch_size = 100    # batch大小设置
    accuracy_cnt = 0    # 正确计数

    for i in range(0, len(images), batch_size):
        x_batch = images[i:i+batch_size]    # 按batch进行切片
        t_batch = labels[i:i+batch_size]

        y_batch = forward(network, x_batch)
        p_batch = np.argmax(y_batch, axis=1)  # 每行取最大索引
        accuracy_cnt += np.sum(p_batch == t_batch)

    accuracy = accuracy_cnt / len(images)
    print(f"Batch Accuracy: {accuracy:.4f}")

3.7 小结

本章介绍了神经网络的前向传播过程。神经网络与上一章的感知机在“按层传递信号”的结构上是一致的，但在信号传递方式上存在显著差异。感知机采用的是具有突变特性的阶跃函数，而神经网络则使用变化平滑的 sigmoid 函数作为激活函数。这一激活函数的差异对神经网络的学习能力至关重要，我们将在下一章中详细探讨其意义。

下一章将深入讲解神经网络的学习机制，内容包括损失函数、反向传播算法以及权重的更新方法，从而揭示神经网络是如何通过训练不断提升性能的。