大语言模型原理与实战(第二章 Transformer 架构——注意力机制)
大语言模型原理与实战(第二章 Transformer 架构——注意力机制)
目录
最近大模型很火,很多朋友想要入门大模型,网上的资料很多,不知道从何开始,非常有幸看到Datawhale开源了大语言模型原理与实战教程——Happy-LLM。
本项目是一个系统性的 LLM 学习教程,将从 NLP 的基本研究方法出发,根据 LLM 的思路及原理逐层深入,依次为读者剖析 LLM 的架构基础和训练过程。同时,该项目结合目前 LLM 领域最主流的代码框架,演练如何亲手搭建、训练一个 LLM。
【教程地址】:Happy-LLM。
第二章 Transformer 架构——注意力机制
什么是注意力机制
- NLP 文本表示方法的演进:NLP 从统计机器学习向深度学习发展,文本表示方法也从基于统计学习模型的向量空间模型、语言模型,经 Word2Vec 的单层神经网络,进入到借助神经网络学习文本表示的阶段。这一转变顺应了技术发展的趋势,为 NLP 任务带来了新的可能性和更高的性能。
- 神经网络核心架构:以计算机视觉为起源的神经网络有前馈神经网络、卷积神经网络和循环神经网络。
- 前馈神经网络每一层神经元与上下层神经元完全连接;
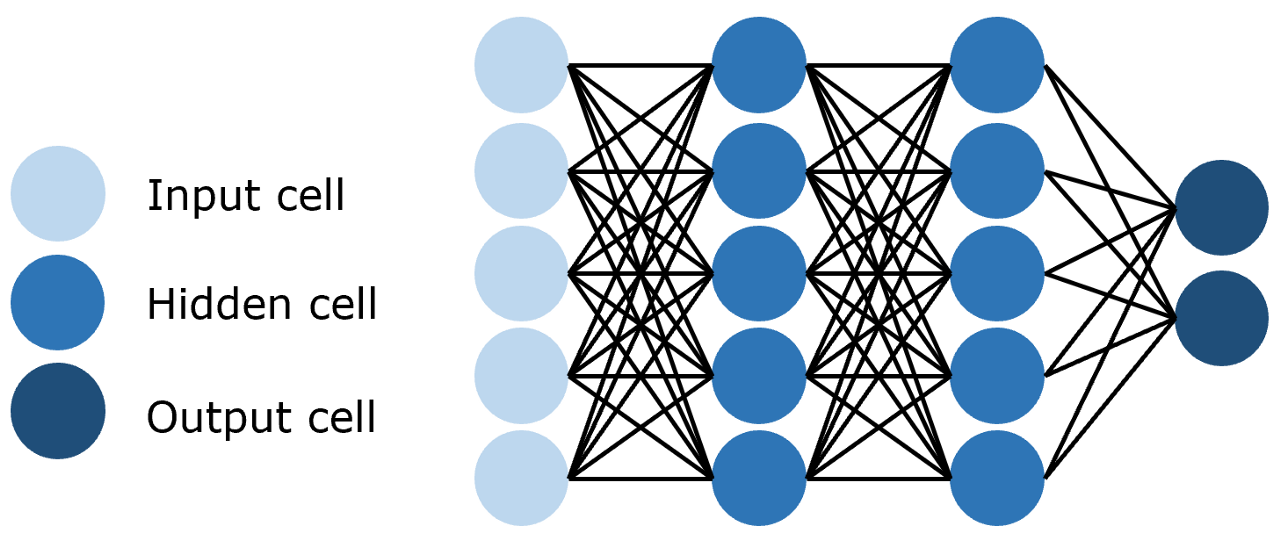
- 卷积神经网络通过卷积层提取特征,训练参数量小于前馈神经网络;
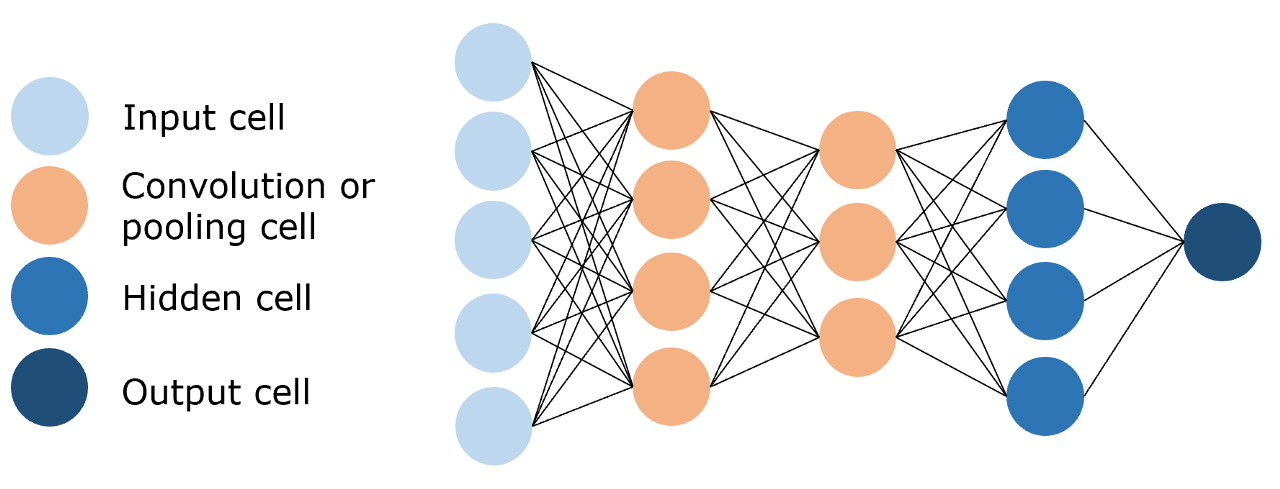
- 循环神经网络能处理序列、时序数据,可利用历史信息。
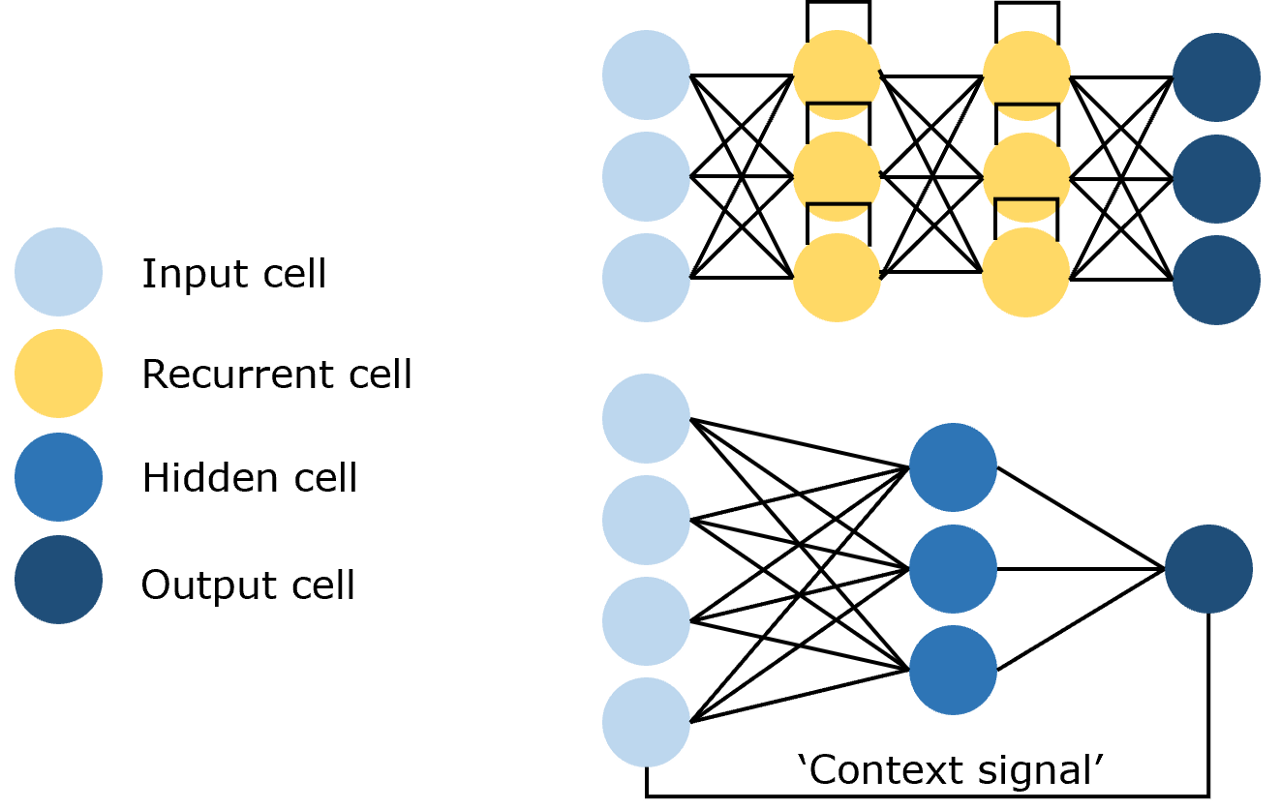
- 前馈神经网络每一层神经元与上下层神经元完全连接;
- RNN 在 NLP 中的地位与缺陷:由于 NLP 处理的文本多为序列,RNN 在 NLP 任务上表现出色,在注意力机制出现前,RNN 及 LSTM 是 NLP 领域的主导。然而,RNN 存在序列依序计算限制计算机并行计算能力,导致计算时间成本高,且难以捕捉长序列相关关系的问题,尽管 LSTM 有所优化,但仍不尽人意。
- Transformer 与注意力机制:为解决 RNN 的问题,Vaswani 等学者借鉴 CV 领域的注意力机制构建了 Transformer。注意力机制源于计算机视觉,核心思想是聚焦重点。其有 Query、Key 和 Value 三个核心变量,通过计算 Query 与 Key 相关性为真值加权求和,拟合序列中词间关系,让注意力机制成为深度学习核心架构之一。
深入理解注意力机制
- 注意力机制核心变量及字典示例:注意力机制存在三个核心变量:即查询值Query、键值Key和真值Value。以字典{"apple":10, "banana":5, "chair":2}为例,字典的键对应注意力机制中的键值Key,字典的值对应真值Value。在精确匹配时,如查询值Query为“apple”,可直接匹配得到对应Value。但当Query为“fruit”这种包含多个Key的概念时,需组合Key对应的Value。
- 注意力分数的引入:为解决包含多个Key概念的查询问题:引入注意力分数概念。当Query为“fruit”时,给“apple”“banana”“chair”分别赋予权重0.6、0.4、0,通过权重与对应值相乘再相加得到最终查询值8。注意力分数表示为查询到Query,赋予每个Key的注意力程度。
- 基于词向量计算注意力分数:利用词向量和点积计算相似度,进而得到注意力分数。第一章提到词向量经训练可表征语义信息,语义相近词在向量空间距离近,语义较远词距离远。可用欧式距离或点积度量词向量相似性,根据词向量定义,语义相似词向量点积大于0,不相似词向量点积小于0。假设Query“fruit”词向量为q,Key词向量堆叠成矩阵K,通过q与K转置相乘得到反映Query与每个Key相似程度的x,再经Softmax层转化为和为1的权重,即注意力分数。
- 注意力机制公式的推导与完善:逐步推导并完善注意力机制公式:首先得到基本公式
,但此时值为标量且只查询一个Query。进一步将值转化为维度为
的向量,多个Query词向量堆叠成矩阵Q,得到
。最后考虑到Q和K维度
较大时对softmax放缩及梯度稳定性的影响,对Q和K乘积结果放缩,得到核心计算公式
。
注意力机制的实现
这里使用Pytorch做一个简单的实现:
'''注意力计算函数'''
def attention(query, key, value, dropout=None):
'''
args:
query: 查询值矩阵
key: 键值矩阵
value: 真值矩阵
'''
# 获取键向量的维度,键向量的维度和值向量的维度相同
d_k = query.size(-1)
# 计算Q与K的内积并除以根号dk
# transpose——相当于转置
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
# Softmax
p_attn = scores.softmax(dim=-1)
if dropout is not None:
p_attn = dropout(p_attn)
# 采样
# 根据计算结果对value进行加权求和
return torch.matmul(p_attn, value), p_attn
自注意力
- 注意力机制本质:注意力机制本质是对两段序列元素依次做相似度计算,找出一个序列每个元素对另一个序列每个元素的相关度,再基于此相关度进行加权,也就是分配注意力。计算过程中的Q、K、V 就来源于这两段序列。在实际应用中,常常只需计算Query和Key之间的注意力结果,较少有额外的真值Value,多数时候只需拟合两个文本序列。
- 经典注意力机制在Transformer Decoder中的应用:在经典注意力机制里,Q通常来自一个序列,K与V来自另一个序列,它们都通过参数矩阵计算得到,以此来拟合两个序列之间的关系。以Transformer的Decoder结构为例,Q来自Decoder的输入,K与V来自Encoder的输出,如此便能拟合编码信息与历史信息间的关系,有助于综合这两种信息来实现未来的预测。
- Transformer Encoder中的自注意力机制:Transformer的Encoder结构采用了注意力机制的变种——自注意力机制。自注意力机制是计算本身序列中每个元素对其他元素的注意力分布,计算时Q、K、V都由同一个输入通过不同的参数矩阵计算得出。在Encoder中,Q、K、V分别是输入与参数矩阵𝑊𝑞、𝑊𝑘、𝑊𝑣做积得到,进而拟合输入语句中每一个token对其他所有token的关系,通过这种方式可以找到一段文本中每一个token与其他所有token的相关关系大小,实现对文本之间依赖关系的建模。在代码实现上,是通过给Q、K、V的输入传入同一个参数,如
来实现自注意力机制。attention(x, x, x)
掩码自注意力
掩码自注意力,即 Mask Self-Attention,是指使用注意力掩码的自注意力机制。掩码的作用是遮蔽一些特定位置的 token,模型在学习的过程中,会忽略掉被遮蔽的 token。使用注意力掩码的核心动机是让模型只能使用历史信息进行预测而不能看到未来信息。使用注意力机制的 Transformer 模型也是通过类似于 n-gram 的语言模型任务来学习的,也就是对一个文本序列,不断根据之前的 token 来预测下一个 token,直到将整个文本序列补全。
例如,如果待学习的文本序列是 【BOS】I like you【EOS】,那么,模型会按如下顺序进行预测和学习:
Step 1:输入 【BOS】,输出 I
Step 2:输入 【BOS】I,输出 like
Step 3:输入 【BOS】I like,输出 you
Step 4:输入 【BOS】I like you,输出 【EOS】理论上来说,只要学习的语料足够多,通过上述的过程,模型可以学会任意一种文本序列的建模方式,也就是可以对任意的文本进行补全。但是,我们可以发现,上述过程是一个串行的过程,也就是需要先完成 Step 1,才能做 Step 2,接下来逐步完成整个序列的补全。我们在一开始就说过,Transformer 相对于 RNN 的核心优势之一即在于其可以并行计算,具有更高的计算效率。如果对于每一个训练语料,模型都需要串行完成上述过程才能完成学习,那么很明显没有做到并行计算,计算效率很低。
针对这个问题,Transformer 就提出了掩码自注意力的方法。掩码自注意力会生成一串掩码,来遮蔽未来信息。例如,我们待学习的文本序列仍然是 【BOS】I like you【EOS】,我们使用的注意力掩码是【MASK】,那么模型的输入为:
<BOS> 【MASK】【MASK】【MASK】【MASK】
<BOS> I 【MASK】 【MASK】【MASK】
<BOS> I like 【MASK】【MASK】
<BOS> I like you 【MASK】
<BoS> I like you </EOS>在每一行输入中,模型仍然是只看到前面的 token,预测下一个 token。但是注意,上述输入不再是串行的过程,而可以一起并行地输入到模型中,模型只需要每一个样本根据未被遮蔽的 token 来预测下一个 token 即可,从而实现了并行的语言模型。
观察上述的掩码,我们可以发现其实则是一个和文本序列等长的上三角矩阵。我们可以简单地通过创建一个和输入同等长度的上三角矩阵作为注意力掩码,再使用掩码来遮蔽掉输入即可。也就是说,当输入维度为 (batch_size, seq_len, hidden_size)时,我们的 Mask 矩阵维度一般为 (1, seq_len, seq_len)(通过广播实现同一个 batch 中不同样本的计算)。
在具体实现中,我们通过以下代码生成 Mask 矩阵:
# 创建一个上三角矩阵,用于遮蔽未来信息。
# 先通过 full 函数创建一个 1 * seq_len * seq_len 的矩阵
mask = torch.full((1, args.max_seq_len, args.max_seq_len), float("-inf"))
# triu 函数的功能是创建一个上三角矩阵
mask = torch.triu(mask, diagonal=1)生成的 Mask 矩阵会是一个上三角矩阵,上三角位置的元素均为 -inf,其他位置的元素置为0。
在注意力计算时,我们会将计算得到的注意力分数与这个掩码做和,再进行 Softmax 操作:
# 此处的 scores 为计算得到的注意力分数,mask 为上文生成的掩码矩阵
scores = scores + mask[:, :seqlen, :seqlen]
scores = F.softmax(scores.float(), dim=-1).type_as(xq)通过做求和,上三角区域(也就是应该被遮蔽的 token 对应的位置)的注意力分数结果都变成了 -inf,而下三角区域的分数不变。再做 Softmax 操作,-inf 的值在经过 Softmax 之后会被置为 0,从而忽略了上三角区域计算的注意力分数,从而实现了注意力遮蔽。
多头注意力
注意力机制可以实现并行化与长期依赖关系拟合,但一次注意力计算只能拟合一种相关关系,单一的注意力机制很难全面拟合语句序列里的相关关系。因此 Transformer 使用了多头注意力机制(Multi-Head Attention),即同时对一个语料进行多次注意力计算,每次注意力计算都能拟合不同的关系,将最后的多次结果拼接起来作为最后的输出,即可更全面深入地拟合语言信息。
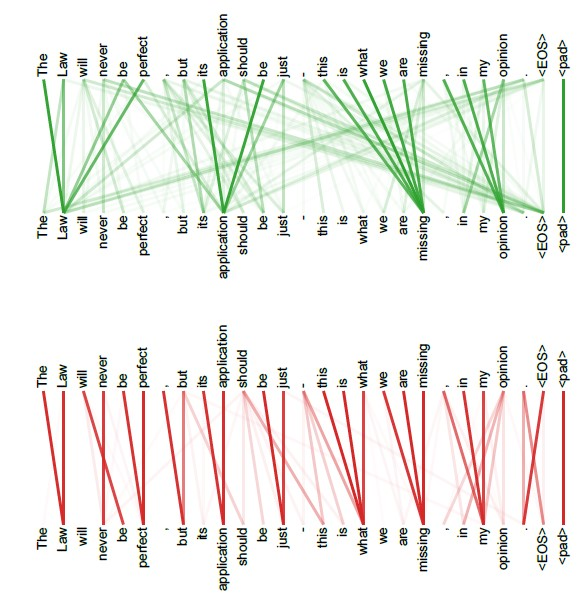
上层与下层分别是两个注意力头对同一段语句序列进行自注意力计算的结果,可以看到,对于不同的注意力头,能够拟合不同层次的相关信息。通过多个注意力头同时计算,能够更全面地拟合语句关系。
事实上,所谓的多头注意力机制其实就是将原始的输入序列进行多组的自注意力处理;然后再将每一组得到的自注意力结果拼接起来,再通过一个线性层进行处理,得到最终的输出。我们用公式可以表示为:

其最直观的代码实现并不复杂,即 n 个头就有 n 组3个参数矩阵,每一组进行同样的注意力计算,但由于是不同的参数矩阵从而通过反向传播实现了不同的注意力结果,然后将 n 个结果拼接起来输出即可。但上述实现时空复杂度均较高,我们可以通过矩阵运算巧妙地实现并行的多头计算,其核心逻辑在于使用三个组合矩阵来代替了n个参数矩阵的组合,也就是矩阵内积再拼接其实等同于拼接矩阵再内积。
具体实现参考如下代码:
import torch.nn as nn
import torch
'''多头自注意力计算模块'''
class MultiHeadAttention(nn.Module):
def __init__(self, args: ModelArgs, is_causal=False):
# 构造函数
# args: 配置对象
super().__init__()
# 隐藏层维度必须是头数的整数倍,因为后面我们会将输入拆成头数个矩阵
assert args.n_embd % args.n_heads == 0
# 模型并行处理大小,默认为1。
model_parallel_size = 1
# 本地计算头数,等于总头数除以模型并行处理大小。
self.n_local_heads = args.n_heads // model_parallel_size
# 每个头的维度,等于模型维度除以头的总数。
self.head_dim = args.dim // args.n_heads
# Wq, Wk, Wv 参数矩阵,每个参数矩阵为 n_embd x n_embd
# 这里通过三个组合矩阵来代替了n个参数矩阵的组合,其逻辑在于矩阵内积再拼接其实等同于拼接矩阵再内积,
# 不理解的读者可以自行模拟一下,每一个线性层其实相当于n个参数矩阵的拼接
self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)
self.wk = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)
self.wv = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)
# 输出权重矩阵,维度为 n_embd x n_embd(head_dim = n_embeds / n_heads)
self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False)
# 注意力的 dropout
self.attn_dropout = nn.Dropout(args.dropout)
# 残差连接的 dropout
self.resid_dropout = nn.Dropout(args.dropout)
# 创建一个上三角矩阵,用于遮蔽未来信息
# 注意,因为是多头注意力,Mask 矩阵比之前我们定义的多一个维度
if is_causal:
mask = torch.full((1, 1, args.max_seq_len, args.max_seq_len), float("-inf"))
mask = torch.triu(mask, diagonal=1)
# 注册为模型的缓冲区
self.register_buffer("mask", mask)
def forward(self, q: torch.Tensor, k: torch.Tensor, v: torch.Tensor):
# 获取批次大小和序列长度,[batch_size, seq_len, dim]
bsz, seqlen, _ = q.shape
# 计算查询(Q)、键(K)、值(V),输入通过参数矩阵层,维度为 (B, T, n_embed) x (n_embed, n_embed) -> (B, T, n_embed)
xq, xk, xv = self.wq(q), self.wk(k), self.wv(v)
# 将 Q、K、V 拆分成多头,维度为 (B, T, n_head, C // n_head),然后交换维度,变成 (B, n_head, T, C // n_head)
# 因为在注意力计算中我们是取了后两个维度参与计算
# 为什么要先按B*T*n_head*C//n_head展开再互换1、2维度而不是直接按注意力输入展开,是因为view的展开方式是直接把输入全部排开,
# 然后按要求构造,可以发现只有上述操作能够实现我们将每个头对应部分取出来的目标
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xq = xq.transpose(1, 2)
xk = xk.transpose(1, 2)
xv = xv.transpose(1, 2)
# 注意力计算
# 计算 QK^T / sqrt(d_k),维度为 (B, nh, T, hs) x (B, nh, hs, T) -> (B, nh, T, T)
scores = torch.matmul(xq, xk.transpose(2, 3)) / math.sqrt(self.head_dim)
# 掩码自注意力必须有注意力掩码
if self.is_causal:
assert hasattr(self, 'mask')
# 这里截取到序列长度,因为有些序列可能比 max_seq_len 短
scores = scores + self.mask[:, :, :seqlen, :seqlen]
# 计算 softmax,维度为 (B, nh, T, T)
scores = F.softmax(scores.float(), dim=-1).type_as(xq)
# 做 Dropout
scores = self.attn_dropout(scores)
# V * Score,维度为(B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
output = torch.matmul(scores, xv)
# 恢复时间维度并合并头。
# 将多头的结果拼接起来, 先交换维度为 (B, T, n_head, C // n_head),再拼接成 (B, T, n_head * C // n_head)
# contiguous 函数用于重新开辟一块新内存存储,因为Pytorch设置先transpose再view会报错,
# 因为view直接基于底层存储得到,然而transpose并不会改变底层存储,因此需要额外存储
output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
# 最终投影回残差流。
output = self.wo(output)
output = self.resid_dropout(output)
return output
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)