深度学习方法:受限玻尔兹曼机RBM(三)模型求解,Gibbs sampling
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld。技术交流QQ群:433250724,欢迎对算法、技术、应用感兴趣的同学加入。本篇重点讲一下RBM模型求解方法,其实用的依然是梯度上升方法,但是求解的方法需要用到随机采样的方法,常见的有:Gibbs Sampling和对比散度(contrastive divergence, CD)算法。RBM
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld。
技术交流QQ群:433250724,欢迎对算法、技术、应用感兴趣的同学加入。
接下来重点讲一下RBM模型求解方法,其实用的依然是梯度优化方法,但是求解需要用到随机采样的方法,常见的有:Gibbs Sampling和对比散度(contrastive divergence, CD[8])算法。
RBM目标函数
假设给定的训练集合是 S={vi} <script type="math/tex" id="MathJax-Element-1">S = \{v^i\} </script>,总数是 ns <script type="math/tex" id="MathJax-Element-2">n_s</script>,其中每个样本表示为 vi=(vi1,vi2,…,vinv) <script type="math/tex" id="MathJax-Element-3">\textbf{v}^{i} = (v_1^i, v_2^i, \dots , v_{n_v}^i)</script>,且都是独立同分布i.i.d的。RBM采用最大似然估计,即最大化
参数表示为 θ=(W,a,b) <script type="math/tex" id="MathJax-Element-5">\theta = (W, \textbf{a}, \textbf{b})</script>,因此统一的参数更新表达式为:
其中, η <script type="math/tex" id="MathJax-Element-7">\eta</script>表示学习速率。因此,很明显,只要我们可以求解出参数的梯度,我们就可以求解RMB模型了。我们先考虑任意单个训练样本( v0 <script type="math/tex" id="MathJax-Element-8">\textbf{v}^0</script>)的情况,即
其中 v <script type="math/tex" id="MathJax-Element-10">\textbf{v}</script>表示任意的训练样本,而 v0 <script type="math/tex" id="MathJax-Element-11">\textbf{v}^0</script>则表示一个特定的样本。
(其中第3个等式左边内条件概率 P(h|v0) <script type="math/tex" id="MathJax-Element-13">P(\textbf{h}|\textbf{v}^0)</script>,因为 e−E(v0,h)∑he−E(v0,h)=e−E(v0,h)/Z∑he−E(v0,h)/Z=P(v0,h)P(v0)=P(h|v0) <script type="math/tex" id="MathJax-Element-14">\frac{e^{-E(\textbf{v}^0,\textbf{h})}}{\sum_{\textbf{h}}e^{-E(\textbf{v}^0,\textbf{h})}} = \frac{e^{-E(\textbf{v}^0,\textbf{h})}/Z}{\sum_{\textbf{h}}e^{-E(\textbf{v}^0,\textbf{h})}/Z} = \frac{P(\textbf{v}^0,\textbf{h})}{P(\textbf{v}^0)} = P(\textbf{h}|\textbf{v}^0)</script>)
上面式子的两个部分的含义是期望——左边是梯度 ∂E(v0,h)∂θ <script type="math/tex" id="MathJax-Element-15">\frac{\partial E(\textbf{v}^0,\textbf{h})}{\partial\theta}</script>在条件概率分布 P(h|v0) <script type="math/tex" id="MathJax-Element-16">P(\textbf{h}|\textbf{v}^0)</script>下的期望;右边是梯度 ∂E(v,h)∂θ <script type="math/tex" id="MathJax-Element-17">\frac{\partial E(\textbf{v},\textbf{h})}{\partial\theta}</script>在联合概率分布 P(h,v) <script type="math/tex" id="MathJax-Element-18">P(\textbf{h},\textbf{v})</script>下的期望。要求前面的条件概率是比较容易一些的,而要求后面的联合概率分布是非常困难的,因为它包含了归一化因子 Z <script type="math/tex" id="MathJax-Element-19">Z</script>(对所有可能的取值求和,连续的情况下是积分),因此我们采用一些随机采样来近似求解。把上面式子再推导一步,可以得到,
因此,我们重点就是需要就算 ∑hP(h|v)∂E(v,h)∂θ <script type="math/tex" id="MathJax-Element-21">\sum_{\textbf{h}}P(\textbf{h}|\textbf{v})\frac{\partial E(\textbf{v},\textbf{h})}{\partial\theta}</script>,特别的,针对参数 W,a,b <script type="math/tex" id="MathJax-Element-22">W, \textbf{a}, \textbf{b}</script>来说,有
类似的,我们可以很容易得到:
于是,我们很容易得到,
上面求出了一个样本的梯度,对于 ns <script type="math/tex" id="MathJax-Element-29">n_s</script>个样本有
到这里就比较明确了,主要就是要求出上面三个梯度;但是因为不好直接求概率分布 P(v) <script type="math/tex" id="MathJax-Element-33">P(\textbf{v})</script>,前面分析过,计算复杂度非常大,因此采用一些随机采样的方法来得到近似的解。看这三个梯度的第二项实际上都是求期望,而我们知道,样本的均值是随机变量期望的无偏估计。
Gibbs Sampling
很多资料都有提到RBM可以用Gibbs Sampling来做,但是具体怎么做不讲(是不是有点蛋疼?),可能很多人也不清楚到底怎么做。下面稍微介绍一下。
吉布斯采样(Gibbs sampling),是MCMC方法的一种,具体可以看我前面整理的随机采样MCMC的文章。总的来说,Gibbs采样可以从一个复杂概率分布 P(X) <script type="math/tex" id="MathJax-Element-498">P(X)</script>下生成数据,只要我们知道它每一个分量的相对于其他分量的条件概率 P(Xk|X−k) <script type="math/tex" id="MathJax-Element-499">P(X_k|X_{-k})</script>,就可以对其进行采样。而RBM模型的特殊性,隐藏层神经元的状态只受可见层影响(反之亦然),而且同一层神经元之间是相互独立的,那么就可以根据如下方法依次采样:
也就是说 hi <script type="math/tex" id="MathJax-Element-500">h_i</script>是以概率 P(hi|v0) <script type="math/tex" id="MathJax-Element-501">P(h_i|\textbf{v}_0)</script>为1,其他的都类似。这样当我们迭代足够次以后,我们就可以得到满足联合概率分布 P(v,h) <script type="math/tex" id="MathJax-Element-502">P(\textbf{v},\textbf{h})</script>下的样本 (v,h) <script type="math/tex" id="MathJax-Element-503">(\textbf{v},\textbf{h})</script>,其中样本 (v) <script type="math/tex" id="MathJax-Element-504">(\textbf{v})</script>可以近似认为是 P(v) <script type="math/tex" id="MathJax-Element-505">P(\textbf{v})</script>下的样本,下图也说明了这个迭代采样的过程: 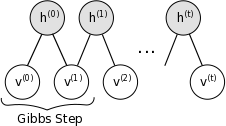
有了样本 (v) <script type="math/tex" id="MathJax-Element-506">(\textbf{v})</script>就可以求出上面写到的三个梯度( ∂LS∂wij,∂LS∂ai,∂LS∂bi <script type="math/tex" id="MathJax-Element-507">\frac{\partial L_S}{\partial w_{ij}} ,\frac{\partial L_S}{\partial a_i} ,\frac{\partial L_S}{\partial b_i} </script>)了,用梯度上升就可以对参数进行更新了。(实际中,可以在k次迭代以后,得到样本集合{ v <script type="math/tex" id="MathJax-Element-508">\textbf{v}</script>},比如迭代100次取后面一半,带入上面梯度公式的后半部分计算平均值。)
看起来很简单是不是?但是问题是,每一次gibbs采样过程都需要反复迭代很多次以保证马尔科夫链收敛,而这只是一次梯度更新,多次梯度更新需要反复使用gibbs采样,使得算法运行效率非常低。为了加速RBM的训练过程,Hinton等人提出了对比散度(Contrastive Divergence)方法,大大加快了RBM的训练速度,将在下一篇重点讲一下。
OK,本篇先到这里。平时工作比较忙,加班什么的(IT的都这样),晚上回到家比较晚,每天只能挤一点点时间写,写的比较慢,见谅。RBM这一块可以看的资料很多,网上一搜一大堆,还包括hinton的一些论文和Bengio的综述[9],不过具体手写出来的思路还是借鉴了[7],看归看,我会自己推导并用自己的语言写出来,大家有什么问题都可以留言讨论。下一篇最后讲一下CD算法,后面有时间再拿code出来剖析一下。
觉得有一点点价值,就支持一下哈!花了很多时间手打公式的说~更多内容请关注Bin的专栏
参考资料
[1] http://www.chawenti.com/articles/17243.html
[2] 张春霞,受限波尔兹曼机简介
[3] http://www.cnblogs.com/tornadomeet/archive/2013/03/27/2984725.html
[4] http://deeplearning.net/tutorial/rbm.html
[5] Asja Fischer, and Christian Igel,An Introduction to RBM
[6] G.Hinton, A Practical Guide to Training Restricted Boltzmann Machines
[7] http://blog.csdn.net/itplus/article/details/19168937
[8] G.Hinton, Training products of experts by minimizing contrastive divergence, 2002.
[9] Bengio, Learning Deep Architectures for AI, 2009
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容

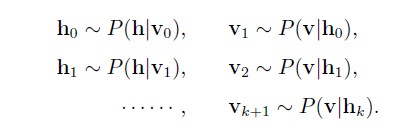





所有评论(0)