点击下方卡片，关注“小白玩转Python”公众号

人工神经元，通常在人工神经网络（ANNs）中被称为节点或单元，是模仿人脑中生物神经元行为的基本单元。这些人工神经元作为神经网络的基本构建块，使网络能够从数据中学习和做出决策。

人工神经元的结构

一个人工神经元通常由以下部分组成：

1. 输入：

每个神经元从多个源接收输入，例如其他神经元或直接从外部数据。这些输入通常是代表数据特征或属性的数值。

2. 权重：

每个输入都与一个权重相关联，该权重代表该输入在影响神经元输出中的强度或重要性。这些权重可以在学习过程中调整，以优化神经元的性能。

3. 求和函数：

神经元计算其输入的加权和。数学上，这表示为：

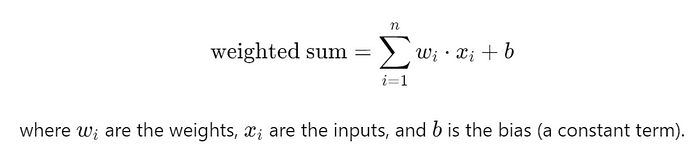
偏置是一个可调参数，加在输入的加权和上，然后通过神经元的激活函数。

• 偏置允许神经元的激活函数独立于输入进行调整。它将整个激活函数向左或向右移动，影响神经元何时被激活或“触发”。这种灵活性帮助神经网络更好地拟合数据，提供了额外的自由度，并在训练过程中学习复杂关系。它还允许网络模拟可能不通过原点（当加权和为零时）的数据模式。

• 像权重一样，偏置通常是随机初始化的，并在训练过程中通过优化算法如梯度下降进行调整。

4. 激活函数：

在计算加权和之后，神经元应用一个激活函数。这个函数引入了神经元输出的非线性，允许神经网络模拟数据中的复杂关系。常见的激活函数包括sigmoid、tanh、ReLU（修正线性单元）和softmax。

5. 输出：

激活函数产生神经元的输出，通常作为输入传递给网络中的其他神经元或用作网络的最终输出。

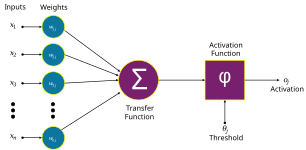
人工神经元在以下方面类似于生物神经元：

• 学习：神经元通过调整其权重来学习，基于其预测输出和实际输出之间的误差（在监督学习中）。这个过程通常通过梯度下降等优化算法实现。

• 特征提取：神经元可以通过适当地加权输入来从复杂数据中提取相关特征。在深度神经网络中，更高级别的神经元学会从低级别神经元的输出中检测更抽象的特征。

• 决策制定：神经元集体根据它们从数据中学到的模式和关系做出决策或预测。这使得神经网络在图像识别、自然语言处理和决策过程中非常有效。

演示

演示了感知器如何根据预测误差使用感知器学习规则更新其权重，通过多个时代迭代来细化其权重，直到学会正确分类给定的数据点。假设我们有一个感知器：

给定数据和预期输出：

感知器学习规则：

epoch 1：

epoch 2：

现在，让我们使用epoch 1中更新的权重重复epoch 2的过程。

在epoch 2中不需要更新权重，因为两个预测都是正确的。

总结：

import numpy as np


class Neuron:
    def __init__(self, num_inputs):
        # Initialize weights randomly and bias to zero
        self.weights = np.random.randn(num_inputs)
        self.bias = 0.0
    
    def sigmoid(self, x):
        # Sigmoid activation function
        return 1 / (1 + np.exp(-x))
    
    def forward(self, inputs):
        # Compute weighted sum of inputs + bias
        weighted_sum = np.dot(inputs, self.weights) + self.bias
        # Apply activation function (sigmoid in this case)
        return self.sigmoid(weighted_sum)

我们用Python创建一个简单的单个人工神经元实现。我们将定义一个Neuron类，代表一个具有输入、权重、偏置、求和函数和激活函数的人工神经元。

说明：

1. 初始化（__init__方法）：

• self.weights：使用np.random.randn(num_inputs)随机初始化权重，其中num_inputs是输入到神经元的数量。

• self.bias：将偏置初始化为零。

2. Sigmoid激活函数（sigmoid方法）：

• 计算sigmoid函数，该函数将输入压缩到(0, 1)范围内，引入非线性。

3. 前向传播（forward方法）：

• 将输入作为数值数组。

• 使用np.dot(inputs, self.weights) + self.bias计算输入的加权和加上偏置。

• 将sigmoid激活函数应用于加权和以产生神经元的输出。

最后：

Create a neuron with 3 inputs
num_inputs = 3
neuron = Neuron(num_inputs)


# Example input vector
inputs = np.array([0.5, -1.0, 2.0])


# Perform forward propagation through the neuron
output = neuron.forward(inputs)


print("Inputs:", inputs) //[ 0.5 -1.   2. ]
print("Output:", output) //0.7808865272523784

虽然人工神经元的基本结构在不同的神经网络架构中保持一致，例如感知器、前馈神经网络、卷积神经网络（CNN）和递归神经网络（RNN），但在如何处理输入、如何在训练期间更新权重以及使用的具体激活函数类型方面可能存在变化。

·  END  ·

🌟 想要变身计算机视觉小能手？快来「小白玩转Python」公众号！

回复“Python视觉实战项目”，解锁31个超有趣的视觉项目大礼包！🎁

本文仅供学习交流使用，如有侵权请联系作者删除