梯度下降是机器学习和深度学习的基础，本身是一个一阶最优化算法，也叫作最优下降法。核心思想是找到使loss值下降最快的方向，按一定的学习率进行逐步探索，直到获取最优解（可能是局部最优解）。要想找到函数的局部极小值，必须向函数上当前点对应梯度的反方向的规定步长距离点进行迭代搜索。如果正方向迭代进行搜索，则会接近函数的局部极大值点，这样的过程称为梯度上升法。

下面我们通过几个例子解释梯度下降及实现

一元函数

我们对下面的一元函数进行分析

f(x) = x^3 + 2*x - 3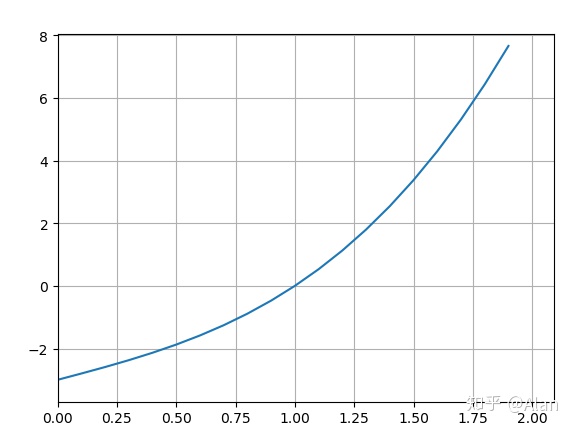

1ad8dcb294fea22aa1d3dde93021ef2d.png

我们研究这个函数，运用代数只是，我们可以很容易的得出 1 是 f(x) = 0的一个解。但是计算机不会进行复杂的代数推演，相比于人脑，计算机拥有更高的运算能力，所以它选择进行逐个值进行尝试，尝试的目标函数为：

loss = (f(x) - 0)^2
即
loss = (x^3 + 2x -3)^2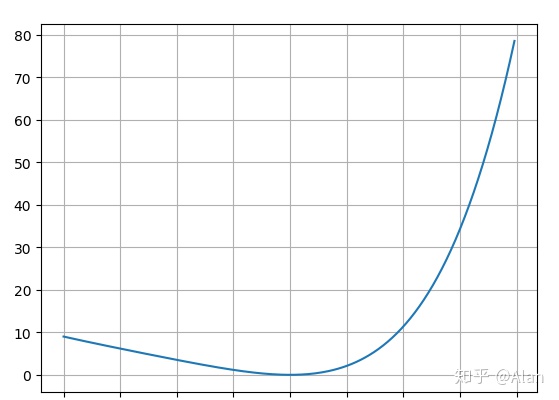

0511320223d81b4b732c3b324245ab5d.png

当error趋近于最小值的时候， 就是 f(x) = 0 在 x 处的解。

通过loss函数的图像，我们可以很容易的看出该函数的最小值即为函数的最低谷。数学上，我们可以通过下面的方式进行求解：

1、对loss函数进行求导

detivative(x) = 6*x^5 + 16*x^3 -18*x^2 + 8*x -12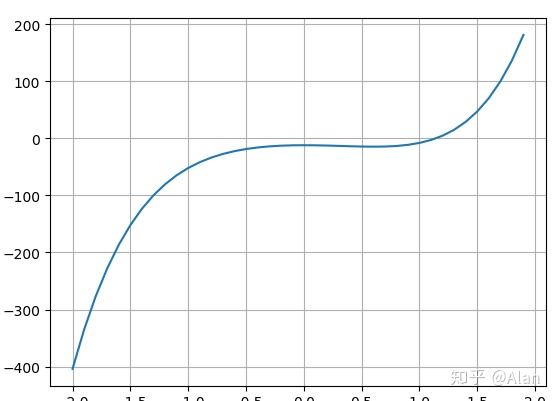

c933cfd4e984cb9bb19acb8fdaaf7c25.png

2、令 derivative(x) = 0 求得X的值，根据 derivative(xI）图像可知：

  • 当 x<1 时， derivative(x)<0 斜率为负
  • 当 x>1 时， derivative(x)>0 斜率为正
  • 当 x逼近1时，derivative(x) 无限趋近于0 斜率为0

3、用 x = x - rate * derivative 代替 x 的迭代移动，（这样表示无论斜率为正或者为负，x 都会像最低点逼近）

针对一元函数这样的简单函数，我们可以通过直观的求出他的倒函数：

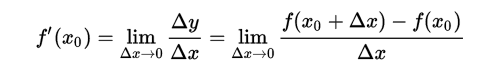
98a8853cfb912e89649ce42faa447d37.png

下面我们依据这个公式来实现梯度下降：

def gradient_descent():
    """
    :return: 梯度下降一维的例子
    """

    def f(x):
        """
        :param x:
        :return: 待解函数
        """
        return x ** 3 + 2 * x - 3

    def error(x, target):
        """
        :param x:
        :return: 误差函数
        """
        return (f(x) - target) ** 2

    def descent(x, target):
        """
        :param x:
        :return: 梯度下降
        """
        delta = 0.00000001
        derivative = (error(x + delta, target) - error(x, target)) / delta
        rate = 0.01
        return x - derivative * rate

    x = 5
    count = 0
    for i in range(500):
        x = descent(x, 0)
        count += 1
        if count % 100 == 0:
            print("x:{:6f}t f(x)={:6f}".format(x, f(x)))

其输出结果如下，可以看到 x 已经趋近于1，可以预见，在迭代步数足够多的情况下，x 会无线趋近于1

d0335bd997ddfac79dcfd0d6dd83ed55.png

多元函数

对于一元函数，我们可以通过上面的方法解决，对于多元函数呢？

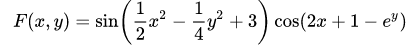
ebf22559ff8a0129c782196876ee697c.png

我们研究下这个函数

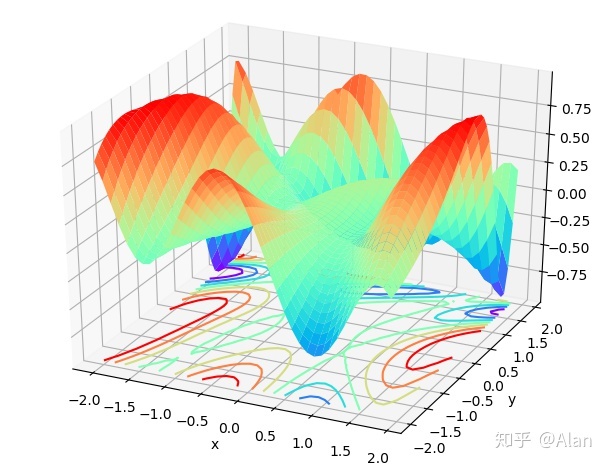
1569d780e3e9d0a41625d29962cbff13.png

对于多元函数来说，我们只需要研究每个变量的偏导数即可，偏导数的概念大学中我们都有学到过，这里不再赘述。同一元函数的逻辑一样，我们使用在每个方向上使用同样的loss函数

def gradient_descent_multi_varible():
    """
    :return: 二元函数的梯度下降
    """

    def f(x, y):
        return np.sin(1 / 2 * np.power(x, 2) - 1 / 4 * np.power(y, 2) + 3) * np.cos(2 * x + 1 - np.power(np.e, y))

    def error(x, y, target):
        return (f(x, y) - target) ** 2

    def descent(x, y, target):
        # 定义delta
        delta = 0.000001
        # 求偏导数斜率
        derivative_x = (error(x + delta, y, target) - error(x, y, target)) / delta
        derivative_y = (error(x, y + delta, target) - error(x, y, target)) / delta

        # 变步长
        rate = 0.02
        x = x - rate * derivative_x
        y = y - rate * derivative_y

        return x, y

    x = random.random()
    y = random.random()
    count = 0
    for i in range(10000):
        x, y = descent(x, y, 0)
        count += 1
        if count % 1000 == 0:
            print("x:{:6f}t y:{:6f}t f(x,y):{:6f}".format(x, y, f(x, y)))

其输出结果如下：

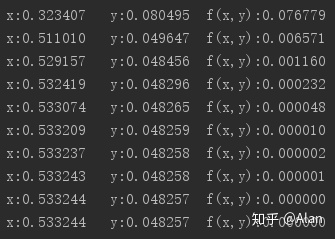
71f93cec572503b15bcee349219c34d3.png

可以看到函数在 x = 0.53324 y=0.04826处 z的取值接近于0

通过上面的描述，我们已经对梯度下降有了一定的了解。现在我们用tensorflow通过梯度下降来拟合函数曲线玩下。

    def add_layer(inputs, in_size, out_size, activation_function=None):
        # 初始化为满足正太分布的随机数
        Weight = tf.Variable(tf.random_normal([in_size, out_size]))
        # 初始化bias
        Bias = tf.Variable(tf.zeros([1, out_size])) + 0.1
        # matmul 为两个矩阵相乘
        Wx_plus_b = tf.matmul(inputs, Weight) + Bias

        if activation_function is None:
            outputs = Wx_plus_b
        else:
            outputs = activation_function(Wx_plus_b)

        return outputs

    # 训练数据准备
    # x 轴为 1 * 300维
    x_data = np.linspace(-1, 1, 300)[:, np.newaxis]
    # 噪音数据 为满足正态分布的 1 * 300维矩阵， 标准差为0.05
    noise = np.random.normal(0, 0.05, x_data.shape)
    y_data = np.square(x_data) - 0.5 + noise

    # 设置占位符
    xs = tf.placeholder(tf.float32, [None, 1])
    ys = tf.placeholder(tf.float32, [None, 1])

    # 网络第一层, 使用relu函数激活
    l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
    # 输出层
    prediction = add_layer(l1, 10, 1, activation_function=None)

    # loss函数
    # reduce_mean为计算tensor上某一维的平均值，主要用来降维
    # reduce_sum 用来计算某一维的和， reduction_indices 为 0 代表列压缩， 1代表行压缩
    loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))

    # 训练, 设置学习率为0.1, 梯度下降优化
    train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

    # 初始化参数
    init = tf.global_variables_initializer()

    # 启动训练
    with tf.Session() as sess:
        # 保存网络结构
        summary_writer = tf.summary.FileWriter("E:python_toolstensorflow_workspacepython_demolog", sess.graph)
        # 绘制拟合过程
        fig = plt.figure()
        ax = fig.add_subplot(1, 1, 1)
        ax.scatter(x_data, y_data)
        plt.show(block=False)

        sess.run(init)
        for i in range(100):
            sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
            prediction_value = sess.run(prediction, feed_dict={xs: x_data})
            # lw参数为粗细
            lines = ax.plot(x_data, prediction_value, "r-", lw=5)
            plt.pause(0.1)

            try:
                ax.lines.remove(lines[0])
            except:
                pass

            if i % 50 == 0:
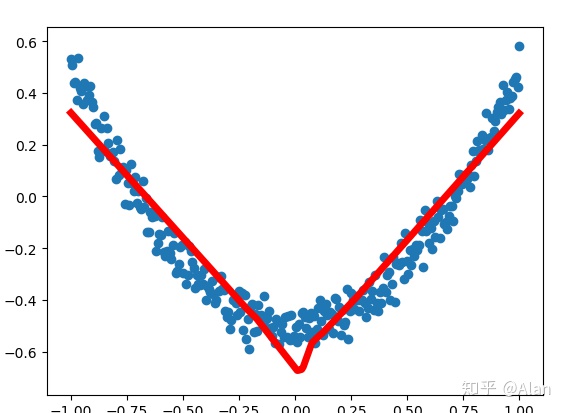
                print(i, sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

这里使用了plt来绘制拟合的过程

ff10601a2ea9e2799e40332f308322f5.png
Logo
九章云极普惠算力

更多推荐

gh_mirrors/core92/core容器化部署：Kubernetes环境下的最佳实践

🚀 作为一款**生产就绪的AI助手框架**，gh_mirrors/core92/core提供了强大的AI对话能力和插件扩展机制。本文将为您详细介绍如何在Kubernetes环境中实现这一AI框架的高效容器化部署，确保系统稳定性和可扩展性。## 🎯 为什么选择Kubernetes部署AI助手框架在当今AI技术快速发展的时代，**容器化部署**已成为企业级应用的标配。Kubernetes作

avatar 九章云极普惠算力

Modern C++ constexpr if：编译时条件实例化的终极指南

现代C++编程中，`constexpr if` 是一个革命性的功能，它允许在编译时根据条件实例化不同的代码路径。这个强大的C++17特性彻底改变了模板编程的方式，让代码更加简洁高效！🚀## 什么是constexpr if？**constexpr if** 是C++17引入的编译时条件语句，它能够在编译期间根据条件选择性地实例化代码块。与传统的`if`语句不同，`constexpr if`

avatar 九章云极普惠算力

如何用OSINT工具保护个人安全：网络骚扰与跟踪防护完全指南

在数字时代，个人安全面临着前所未有的挑战。网络骚扰、在线跟踪和信息泄露已成为许多人面临的现实威胁。开源情报（OSINT）不仅是安全专家的工具，更是每个人保护自己免受网络威胁的必备技能。本文将为你详细介绍如何利用OSINT工具和技巧来防范网络骚扰与跟踪，确保你的数字生活安全无忧。😊## 🤔 什么是OSINT及其在个人安全中的作用开源情报（OSINT）是指从公开可获取的来源收集和分析信息的

avatar 九章云极普惠算力