---

动手学深度学习 - 优化算法 - 12.3 梯度下降

在本节中，我们将深入探讨深度学习中的基础优化方法——梯度下降（Gradient Descent）。虽然在现代神经网络中更常见的是它的变体如小批量随机梯度下降（Mini-batch SGD）或 Adam 等自适应算法，但理解梯度下降对于掌握优化理论、调参技巧以及后续优化算法的演化具有基础性的意义。

---

12.3.1 一维梯度下降

一阶泰勒展开与下降方向

设目标函数 f(x)f(x) 连续可导，令 xx 为当前参数点。基于泰勒展开公式，我们有：

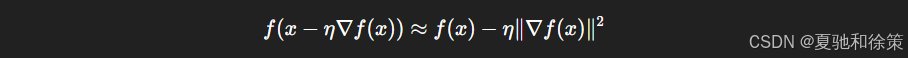
说明：只要选择合适的学习率 η\eta，向负梯度方向更新就能使目标函数单调减小。

代码示例：最小化 f(x)=x2f(x) = x^2

def f(x): return x**2
def f_grad(x): return 2 * x

通过迭代：

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(x)
    return results

我们可以用图像直观展示下降路径。

📘 理论理解：

• 梯度方向表示函数最快下降方向，泰勒展开一阶近似说明沿负梯度方向前进可以减小目标函数值。

• 公式 x←x−η∇f(x)x \leftarrow x - \eta \nabla f(x)x←x−η∇f(x) 是最基本的更新方式，其中 η\etaη 是学习率，控制步长。

• 学习率过大导致发散，过小则收敛缓慢。

🏢 大厂实战理解：

• Google Brain 在早期训练大型 Transformer 时曾因学习率设置不合理导致模型 Loss 发散，最终引入 Warmup 策略避免初期不稳定。

• 字节跳动 推荐团队在 CTR 模型训练中采用逐步缩小的 Learning Rate Schedule（例如 Step Decay 或 Cosine）来提升收敛稳定性。

 

---

12.3.1.1 学习率

学习率 η\eta 是超参数。取值过小，收敛极慢；取值过大，则可能越过最优点甚至发散。

实验对比如下：

• η=0.05\eta = 0.05：收敛极慢

• η=1.1\eta = 1.1：严重发散

这说明，学习率的选择是影响训练效果的核心因素之一。

---

12.3.1.2 局部最小值

若目标函数是非凸的，如 f(x)=x⋅cos⁡(0.15πx)f(x) = x \cdot \cos(0.15\pi x)，则不同初始点与学习率组合可能导致算法陷入局部最优而非全局最优。

📘 理论理解：

• 梯度向量是各个维度方向的偏导数组成，它指向目标函数上升最快的方向，负梯度则为下降最快方向。

• 多维优化问题通过同时更新所有维度参数来逼近极值点。

• 函数表面形状（等高线图）可视化帮助理解更新路径。

🏢 大厂实战理解：

• OpenAI 在训练 GPT 模型时对多个维度参数进行高效更新，其中每个参数梯度可能不同，需要精细化调节。

• NVIDIA 在 DALI（数据预处理库）中曾分析图像增强操作对多变量目标函数的梯度传播影响，以提升训练稳定性。

 

---

12.3.2 多变量梯度下降

将变量从一维推广到高维空间时，我们引入梯度向量 ∇f(x)\nabla f(\mathbf{x})：

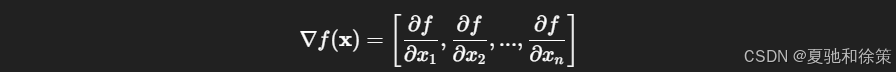
更新公式如下：

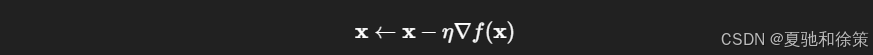
代码示例目标函数为 f(x1,x2)=x12+2x22f(x_1, x_2) = x_1^2 + 2x_2^2，梯度为 (2x1,4x2)(2x_1, 4x_2)。

---

12.3.3 自适应方法

12.3.3.1 牛顿方法

当我们不仅使用一阶导数，还引入二阶导数（Hessian 矩阵）时，我们得到更精确的更新方向：

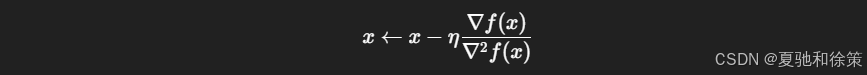
这在凸函数下能加快收敛，但在非凸场景中若 Hessian 为负，则更新方向可能使损失变大。

改进策略：

• 使用 Hessian 的绝对值

• 限制学习率

12.3.3.1 牛顿方法

📘 理论理解：

• 牛顿法利用二阶导数（Hessian）提供函数曲率信息，实现比一阶方法更快的收敛。

• 对凸函数尤其有效，一步收敛是理想情形；但对非凸函数可能因 Hessian 为负而走向错误方向。

🏢 大厂实战理解：

• Google 曾在 BERT 的 pretraining 中研究二阶优化器的收敛曲线，虽理论优越，但计算代价太高，仅用于小模型研究。

• NVIDIA AI Research 用牛顿法分析 Loss 曲率变化，作为调研自适应优化器的重要依据。

 

---

12.3.3.2 收敛分析

若函数在某点附近三阶可导，且 Hessian 非零，则可证明牛顿法具有 二次收敛速度。即误差平方级减少，远快于普通梯度下降的线性收敛。

📘 理论理解：

• 牛顿法具备理论上的二次收敛速度，即误差呈指数下降。

• 关键前提：Hessian 可逆，目标函数足够平滑，当前点处在收敛区域内。

🏢 大厂实战理解：

• 微软亚洲研究院 曾分析机器翻译任务中不同优化算法的收敛区域，发现部分参数初始值差异会严重影响收敛区间进入速度。

 

---

12.3.3.3 预处理

Hessian 全矩阵计算代价极高，因此实际应用中通常只计算对角线项（对角近似）作为预处理矩阵。换言之，不同维度使用不同学习率。该思想是 Adam 和 RMSProp 等方法的理论基础。

📘 理论理解：

• 预处理方法通过缩放不同维度的学习率，使高维空间中各维更新更协调。

• 对角线 Hessian 作为预条件矩阵，是一种近似但实用的方法。

🏢 大厂实战理解：

• 字节跳动数据部门 在搜索排序模型中大量使用带预处理的 Adagrad 或 AdamW 进行训练，解决点击率预测中的稀疏特征权重更新问题。

 

---

12.3.3.4 使用线搜索进行梯度下降

线搜索方法结合解析方向和搜索长度，利用二分查找等策略确定最优步长，可加速收敛。然而其代价在深度学习中较高，因为每步都需遍历全部数据，故一般仅用于传统优化问题。

📘 理论理解：

• 线搜索是求解每一步最优学习率的一种策略，通过最小化目标函数在当前方向上的值找到最佳步长。

• 优点是每次更新最优，缺点是代价高，不适合深度学习中的大规模迭代。

🏢 大厂实战理解：

• OpenAI 在强化学习（如 PPO）中曾尝试引入线搜索策略提高策略更新的稳定性，但因效率问题最终未采用该策略。

• Google JAX 团队 在自动微分和线性规划场景中利用线搜索对函数进行精调，用于解决稀疏约束下的最优解问题。

 

---

12.3.4 小结

• 梯度下降是理解更复杂优化算法的基础。

• 学习率选择对训练过程影响极大。

• 牛顿法具有更快收敛速度，但对非凸问题存在不稳定性。

• 预处理和自适应调整是提高训练效率的关键策略。

• 深度学习中常用方法（如 Adam、RMSProp）均为对基本梯度下降的改进。

---

12.3.5 练习

1. 调整目标函数与学习率，观察不同情况下梯度下降的收敛行为。

2. 实现线搜索算法，结合一维凸函数验证收敛速度。

3. 构造一个函数，使梯度下降非常缓慢（如不同坐标尺度差异巨大）。

4. 使用对角 Hessian 作为预处理因子，观察对收敛的影响。

5. 对比不同优化方法在多个目标函数下的收敛表现。

📘 理论理解：

• 梯度下降是最基础的优化方法，也是后续算法如 Momentum、Adam 的基础。

• 学习率控制收敛速度与稳定性。

• 牛顿法和预处理是对梯度方向与尺度的提升方案。

🏢 大厂实战理解：

• 大厂深度学习平台基本都默认支持 SGD、Adam、RMSProp 等多种优化器，自动调整参数。

• 工程实战中，组合优化策略成为主流，如 Warmup + CosineDecay + AdamW 组合在 Transformer 模型中极其常见。

 

好的，以下是配合《动手学深度学习 - 优化算法 - 12.3 梯度下降》章节内容，精心设计的大厂面试题与参考答案，涵盖理论考察、代码理解、工程应用、陷阱辨析等维度，贴近 Google、字节跳动、OpenAI、NVIDIA 等实际面试风格。

---

面试题：

---

🧠 基础理论类

Q1：什么是梯度下降？它与随机梯度下降的主要区别是什么？

• 考察点：基础概念理解

• 参考答案：

  • 梯度下降（Gradient Descent）是一种迭代优化算法，每次沿着目标函数梯度的负方向更新参数，以最小化损失函数。

  • 全量梯度下降（Batch GD）每次使用整个数据集计算梯度，更新慢但稳定。

  • 随机梯度下降（SGD）每次使用一个样本进行更新，速度快但波动大；小批量梯度下降（Mini-batch SGD）是两者折中。

---

🔍 数学推导类

Q2：请推导梯度下降的一阶泰勒展开，并说明为何沿负梯度方向更新会减小目标函数值？

• 考察点：公式理解与推导能力

• 参考答案：

  • 一阶泰勒展开：

    

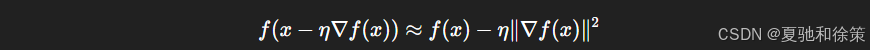
  • 因为 ∥∇f(x)∥2>0\|\nabla f(x)\|^2 > 0，故若 η>0\eta > 0，沿负梯度方向更新将减小 f(x)f(x)。

---

💻 代码能力类（PyTorch）

Q3：你如何用 PyTorch 实现一个一维目标函数的梯度下降？请写出完整代码并解释每行含义。

• 考察点：实际动手能力

import torch

def f(x): return x**2
def f_grad(x): return 2 * x

x = torch.tensor(10.0)
eta = 0.1
for i in range(10):
    grad = f_grad(x)
    x -= eta * grad
print(x)

• 解释：定义目标函数和导数，用固定步长迭代更新参数 x。迭代后 xx 会趋向 0。

---

⚙️ 工程实战类

Q4：在工业级深度学习项目中，你如何选择初始学习率？你用过哪些策略来自动调整学习率？

• 考察点：调参经验与实践策略

• 参考答案：

  • 初始学习率常根据经验或 grid search 选取，如：0.1, 0.01, 0.001。

  • 常见自动调整策略包括：

    • StepLR：每隔 N 轮衰减学习率。

    • CosineAnnealingLR：余弦函数周期性调整。

    • Warmup：训练初期缓慢提升学习率，避免不稳定。

    • ReduceLROnPlateau：监测验证集 loss，停止下降则调小学习率。

  • Google BERT、OpenAI GPT 等都采用 Warmup + Cosine 组合策略。

---

🧱 陷阱识别类

Q5：使用梯度下降时模型 loss 忽高忽低甚至发散，可能是什么原因？如何排查？

• 考察点：实战中的调试能力

• 参考答案：

  • 原因可能有：

    • 学习率过大，导致更新跨越极小值点。

    • 梯度爆炸（尤其在深层网络或 RNN 中）。

    • 数据标准化不足，输入分布不均衡。

  • 排查建议：

    • 使用梯度裁剪（Gradient Clipping）

    • 尝试小学习率重新训练

    • 加入 BatchNorm 或 LayerNorm

    • 可视化 loss 曲线或权重变化趋势

---

🧮 拓展理解类

Q6：请简要比较牛顿法与梯度下降的优缺点。工业界是否常用牛顿法？为什么？

• 考察点：优化方法综合理解

• 参考答案：

  • 优点：牛顿法引入 Hessian 矩阵，收敛速度更快（理论上二次收敛），对凸函数尤为有效。

  • 缺点：Hessian 计算复杂，对非凸函数不稳定，易产生错误更新方向。

  • 实际应用中很少直接使用牛顿法，除非是小规模问题或已知精确 Hessian 的场景（如传统优化或线性模型）。

---

🧠 开放问答类

Q7：你是否能设计一个函数，使得梯度下降法在某些坐标轴上收敛极慢？请解释原理。

• 考察点：理解优化几何形状与学习率适配

• 参考答案：

  • 函数示例：f(x,y)=0.01x2+100y2f(x, y) = 0.01x^2 + 100y^2

  • 原因：在 x 方向梯度极小，更新缓慢；在 y 方向梯度极大，更新易跳跃或发散，形成 长条形等高线，这就是 病态优化面（ill-conditioned surface）。

以下是围绕《动手学深度学习 - 优化算法 - 12.3 梯度下降》章节内容，设计的高质量大厂场景题（Application Scenario Questions），涵盖真实工程中可能遇到的问题，贴近 Google、字节跳动、NVIDIA、OpenAI 等一线公司的项目背景，帮助你锻炼实际工程思维与问题解决能力。

---

🏢 场景题

---

✅ 场景一：Google – 大规模模型预训练中 loss 不收敛

📌 背景：

你参与 Google 的 PaLM 模型训练，发现训练初期 loss 曲线剧烈波动并最终发散。模型使用的是标准的 Transformer 架构，优化器为 SGD，初始学习率设置为 0.1。

🎯 问题：

1. 请分析可能导致 loss 发散的原因。

2. 提出三种解决方案以缓解该问题，并说明背后的原理。

3. 如果你决定用 Warmup + Cosine 学习率策略，请写出实现伪代码。

✅ 参考要点：

• 原因：初始学习率过高；梯度爆炸；参数初始化不当；激活函数饱和。

• 解决方案：

  • 使用 Warmup，前 N 步逐渐升高学习率，防止震荡。

  • 使用 AdamW 替代 SGD，提升早期收敛性。

  • 引入 LayerNorm 或 BatchNorm 稳定梯度传播。

• Warmup + Cosine 伪代码：

def get_lr(step, warmup_steps, base_lr, total_steps):
    if step < warmup_steps:
        return base_lr * step / warmup_steps
    else:
        return base_lr * 0.5 * (1 + cos(pi * (step - warmup_steps) / (total_steps - warmup_steps)))

---

✅ 场景二：字节跳动 – 多目标广告模型优化

📌 背景：

你在字节跳动负责多目标广告 CTR+CVR 联合建模，发现模型对点击率（CTR）收敛良好，但转化率（CVR）loss 下降极慢，训练时间远超预期。

🎯 问题：

1. 为何 CVR 目标可能收敛缓慢？

2. 你如何使用梯度预处理或多尺度学习率机制改进优化速度？

3. 请设计一个多目标任务中基于梯度范数的学习率调节策略。

✅ 参考要点：

• 原因：CVR 样本稀疏，导致梯度更新不频繁；学习率不适配。

• 方案：

  • 对 CVR 分支使用更大的学习率；

  • 使用对角预处理（如 Adagrad）按梯度历史自动缩放；

  • 动态根据梯度范数分配权重。

---

✅ 场景三：NVIDIA – Edge AI 模型训练中 Learning Rate 崩溃

📌 背景：

你在 NVIDIA 的 Jetson 平台上部署一个小型图像识别模型，在训练中出现 accuracy 波动大、loss 上下抖动的情况。硬件为 Jetson Orin Nano，使用自定义数据集。

🎯 问题：

1. 推测梯度下降中可能出现的数值稳定性问题。

2. 你会如何利用学习率调度器（如 ReduceLROnPlateau）优化边缘训练过程？

3. 若采用牛顿法理论指导设计优化策略，你将注意哪些工程实现挑战？

✅ 参考要点：

• 问题分析：学习率不适配；边缘设备精度有限（float16）；参数更新震荡。

• 解决方案：

  • 使用精度安全的优化器如 RMSProp；

  • 训练过程中监控 val loss，自动减少 lr；

  • 牛顿法虽然理想，但边缘设备内存不足，不能计算 Hessian，改用近似方案（如 quasi-Newton）。

---

✅ 场景四：OpenAI – 多层 RNN 梯度下降异常缓慢

📌 背景：

你在 OpenAI 负责训练多层 RNN 模型用于语音生成任务，发现即使使用标准梯度下降，loss 几乎不下降，甚至在前 20 轮变化极小。

🎯 问题：

1. RNN 中的梯度下降缓慢可能是什么原因？

2. 你将如何使用梯度预处理（如使用 RMSProp）或梯度裁剪解决该问题？

3. 请写出一个 RMSProp 更新规则的公式，并解释其物理含义。

✅ 参考要点：

• 问题分析：梯度消失（尤其在 sigmoid/tanh 激活下），导致长期依赖难以捕获。

• 策略：

  • 使用 RMSProp 自适应调整每个维度的更新幅度；

  • 加入梯度裁剪（例如裁剪阈值 5）避免梯度爆炸；

• RMSProp 公式：

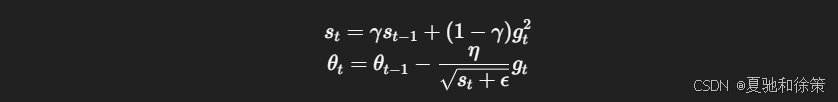
含义：用历史梯度平方的指数加权平均作为缩放因子，防止更新过大。

---

✅ 场景五：腾讯 – 推荐系统训练中陷入局部最优

📌 背景：

你在腾讯负责训练一个基于 DLRM 的推荐系统，初始 loss 下降后很快停滞，经过 100 epoch 仍无实质优化，判断已陷入局部最优。

🎯 问题：

1. 在非凸目标函数下，梯度下降陷入局部最优的可能性如何产生？

2. 你打算用哪种策略跳出局部最优（如加噪声、多模型扰动、重新初始化等）？

3. 如果用牛顿法优化该系统，你如何规避非凸问题中的不稳定性？

✅ 参考要点：

• 原因：参数初始化不佳；训练策略单一；learning rate schedule 不合理。

• 跳出方法：

  • 在多个初始化中挑选最好结果（多起点训练）；

  • 在局部最优附近加入微小扰动；

  • 增加数据扰动（如 dropout、数据增强）提升泛化；

• 牛顿法防坑：

  • 取 Hessian 的绝对值；

  • 加上 damping 正则项；

  • 限制更新步长。

---

以上就是对“梯度下降”这一节的完整解读。下一节我们将进入深度学习中更实用的一种优化策略 —— 随机梯度下降（SGD）。