1.线性回归的基本假定

1. 所有解释变量之间互不相关（无多重共线性）
2. 假设变量（偏差）与随机变量不相关
3. 随机扰动项满足正太分布
4. 数据基本服从线性回归

2.一元线性回归[数据计算方式]

2.1 批量输入 and 批量计算

下部程序中在进行最后的数值迭代过程中，使用的是批量计算的方式进行计算

优点：一次性将所有数据加载到内存中，让计算模型在短时间内对数据进行处理

缺点：当数据量变大，数据变得更加的繁杂，回归结果会出现问题

np.random.randn(50)：

 np.random.randn(100):

import os
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"


# 生成标准正态分布随机数
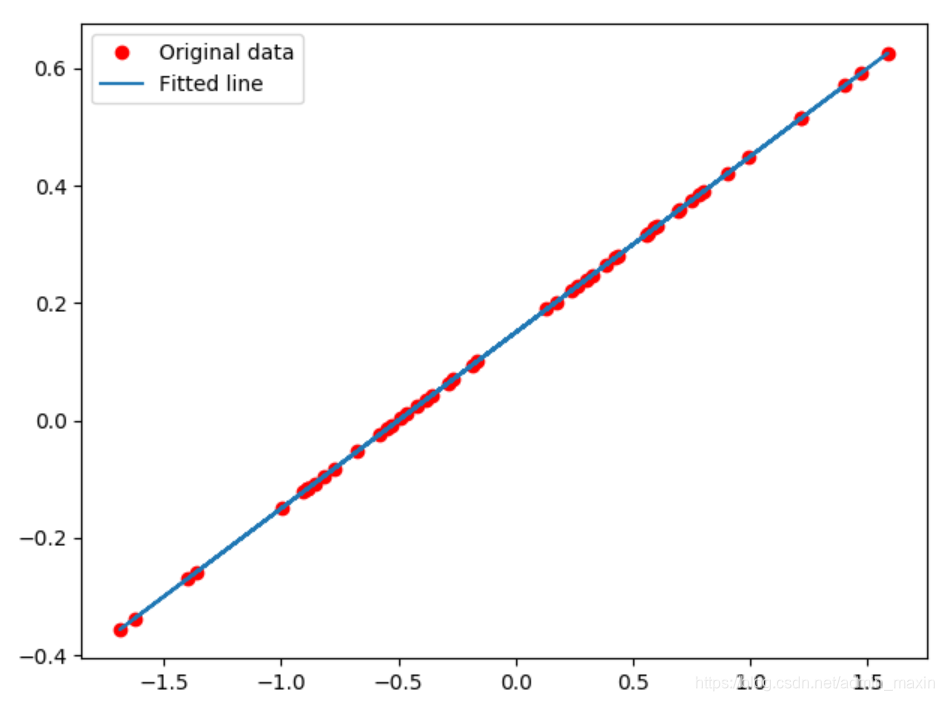
x_data = np.random.randn(50)
# x_data = np.random.randn(100)
y_data = x_data * 0.3 + 0.15

weight = tf.Variable(0.5)
bias = tf.Variable(0.0)

y_model = weight * x_data + bias

loss = tf.pow((y_model - y_data), 2)
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(loss)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

for _ in range(100):
    # 批量计算
    sess.run(train_op)
    print(weight.eval(sess), bias.eval(sess))

plt.plot(x_data, y_data, "ro", label="Original data")
plt.plot(x_data, sess.run(y_model), label="Fitted line")
plt.legend()
plt.show()

1.2 逐个输入 and 逐个计算

import tensorflow as tf
import os
import matplotlib.pyplot as plt
import numpy as np
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"


threshold = 1.0e-2

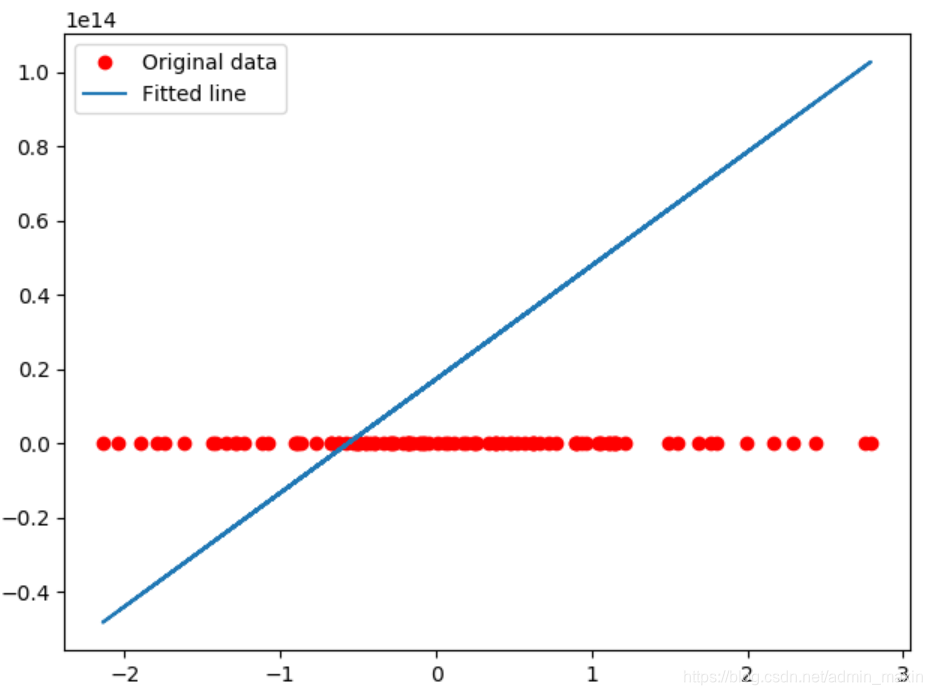
x_data = np.random.randn(100).astype(np.float32)
y_data = x_data * 3 + 1

weight = tf.Variable(1.)
bias = tf.Variable(1.)
x_ = tf.placeholder(tf.float32)  # 输入值
y_ = tf.placeholder(tf.float32)  # 真实值
# y_model = weight * x_ + bias     # 预测值
y_model = tf.add(tf.multiply(x_, weight), bias)

# loss = tf.pow((y_model - y_), 2)
# 提高模型效率
loss = tf.reduce_mean(tf.pow((y_model - y_), 2))
train_op = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)

with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)

    flag = True
    while flag:
        # zip: 返回两个iter的组合元组
        # 逐个输入输入
        for (x, y) in zip(x_data, y_data):
            sess.run(train_op, feed_dict={x_: x, y_: y})
        print("weight:", weight.eval(sess), "| bias:", bias.eval(sess))

        # 当损失值小于阙值threshold时停止模型训练
        if sess.run(loss, feed_dict={x_: x_data, y_: y_data}) <= threshold:
            flag = False

    plt.plot(x_data, y_data, "ro", label="Original data")
    plt.plot(x_data, sess.run(y_model, feed_dict={x_: x_data, y_: y_data}), label="Fitted line")
    plt.legend()
    plt.show()

2.多元线性回归

import numpy as np
import os
import matplotlib.pyplot as plt
import tensorflow as tf
from mpl_toolkits.mplot3d import Axes3D
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"


houses = 100
features = 2

x_data = np.zeros([houses, 2])
for i in range(houses):
    x_data[i, 0] = np.round(np.random.uniform(50., 150.))
    x_data[i, 1] = np.round(np.random.uniform(3., 7.))
weights = np.array([[2.], [3.]])
y_data = np.dot(x_data, weights)

x_data_ = tf.placeholder(tf.float32, [None, 2])
y_data_ = tf.placeholder(tf.float32, [None, 1])
weights_ = tf.Variable(np.ones([2, 1]), dtype=tf.float32)
y_model = tf.matmul(x_data_, weights_)

loss = tf.reduce_mean(tf.pow((y_model - y_data_), 2))

# 学习速率的设置要多加小心
train_op = tf.train.GradientDescentOptimizer(0.0001).minimize(loss)

# with tf.Session() as sess:
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

for _ in range(10):
    for x, y in zip(x_data, y_data):
        z1 = x.reshape(1, 2)
        z2 = y.reshape(1, 1)
        sess.run(train_op, feed_dict={x_data_: z1, y_data_: z2})
    print(weights_.eval(sess))

3.逻辑回归

重点：

1. 逻辑回归并不是回归算法，而是无监督学习中的一种重要的分类算法
2. 逻辑回归返回的结果是一个整数，而线性回归返回的是一个符合实际的预测数值
3. 对于二维图像，逻辑回归的特征是一个二维矩阵，而线性回归的特征是一个一个的列向量
4. 对于损失函数，逻辑回归是预测结果的正确或错误的比较，而线性回归则是预测值与真实值差值之间的比较
5. 逻辑回归常用于二分类中

3.1 特征变换

numpy.ndarray.flatten(order="C"): 将矩阵转换为一维矩阵

order:

C（按列进行转换）

F（按行进行转换）

A（如果a在内存中是Fortran连续的，则表示按列-大数顺序扁平，否则为行-主要顺序）

K（‘k’的意思是按内存中元素出现的顺序使a变平）

import tensorflow as tf
import os
import numpy as np
import cv2
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"


# img = cv2.imread("pic\\001\\pic_0000.jpg", cv2.IMREAD_GRAYSCALE)
img = np.array([[1, 2, 3], [4, 5, 6]])
print(type(img))
print(img.shape)       # (100, 100)

# 特征变换
img_line = img.flatten(order="C")  # [1, 2, 3, 4, 5, 6]
img_line = img.flatten(order="F")  # [1, 4, 2, 5, 3, 6]
print(img_line)
print(type(img_line))

3.2 结果转换

对于线性回归来说，其生成值为某一个取值范围内的任意一个数值，即本身就是一条特定的曲线，通过确定特征值能够很好的在曲线上找到对应的值，而逻辑回归的生成值是一系列非连续的数值。

为了解决生成值的非连续性问题，逻辑回归的结果被转换成了单独的向量，向量中的元素代表着逻辑回归应当属于的分类，每一个数据元素都对应着一个概率，其概率有大小之分，概率得分最高的元素则被认定为其分类结果。

3.3 损失函数

one-hot编码：将不同的类型转化成相同维数的向量

交叉熵：（y:真实的输出值，a:模型的模拟值）

softmax激活函数：（元素所在队列中元素与所有元素指数和的比值）

逻辑回归损失函数：（Y:真实结果转换成one-hot的向量；yi: 模型计算值）

3.4 逻辑回归：胃癌转移判断

数据集：shape(100, 7)

label=tf.stack([col1, col2])

features=tf.stack([col3, col4, col5, col6, col7])

import tensorflow as tf
import numpy as np
import os
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"


def readFile(filename):
    filename_queue = tf.train.string_input_producer(filename, shuffle=False)

    # 定义reader(逐行读取)
    reader = tf.TextLineReader(skip_header_lines=1)
    key, value = reader.read(filename_queue)

    # 读取数据时对应的匹配类型
    # [1.0]:float
    # [1]:int
    # ["null"]:string
    record_defaults = [[1.0], [1.0], [1.0], [1.0], [1.0], [1.0], [1.0]]
    # record_defaults = []
    # for i in range(7):
    #     record_defaults.append([1.0])
    col1, col2, col3, col4, col5, col6, col7 = tf.decode_csv(value, record_defaults=record_defaults)

    # tf.stack：按照给定方向堆叠
    label = tf.stack([col1, col2])
    features = tf.stack([col3, col4, col5, col6, col7])

    # 注意min_after_dequeue < capacity
    example_batch, label_batch = tf.train.shuffle_batch([features, label], batch_size=3, capacity=100, min_after_dequeue=10)
    return example_batch, label_batch


if "__main__" == __name__:
    example_batch, label_batch = readFile(["cancer.txt"])

    weight = tf.Variable(np.random.rand(5, 1).astype(np.float32))
    bias = tf.Variable(np.random.rand(3, 1).astype(np.float32))
    x_ = tf.placeholder(tf.float32, [None, 5])

    # 调用softmax激活函数
    y_model = tf.nn.softmax(tf.matmul(x_, weight) + bias)
    y = tf.placeholder(tf.float32, [3, 2])

    # 损失函数：交叉熵
    loss = -tf.reduce_mean(y*tf.log(y_model))
    train = tf.train.GradientDescentOptimizer(0.01).minimize(loss)

    with tf.Session() as sess:
        sess.run(tf.group(tf.local_variables_initializer(), tf.global_variables_initializer()))
        # 数据读取必须要创建线程协调器
        coord = tf.train.Coordinator()
        threads = tf.train.start_queue_runners(sess=sess, coord=coord)

        flag = 1
        while flag:
            e_val, l_val = sess.run([example_batch, label_batch])
            sess.run(train, feed_dict={x_: e_val, y: l_val})
            if sess.run(loss, feed_dict={x_: e_val, y: l_val}) <= 0:
                flag = 0
            print(sess.run(weight))

        # coord.request_stop()
        # coord.join(threads)