操作环境：

MATLAB 2024a

1、算法描述

在整个OFDM-QPSK系统中，信道模型与信道估计算法是决定通信性能的两大核心因素。系统本质上是一种多载波调制方案，通过将高速数据流分割到多个子载波上并行传输来抵抗频率选择性衰落与符号间干扰。而QPSK调制则是一种相位键控方式，利用相位的四种组合同时携带两位信息，从而在保持较高频谱效率的同时保证一定的抗噪声能力。在这样一个框架下，信道环境的不同与估计方式的差异会对系统的误符号率与误比特率产生深远影响。

首先从信道模型角度来看，系统一般在三种典型的无线多径环境下进行性能验证：ETU、EPA与EVA。这三者均来自3GPP的标准化定义，用于模拟不同的移动通信场景。ETU代表极端城市传播环境，具有大量反射与较长的时延扩展；EPA则为较为理想的低速城市或郊区信道，路径数较少，时延分布集中；EVA介于两者之间，代表中等速度的车辆移动或复杂城市边缘场景。它们的区别并不仅在于路径数量和时延的不同，更在于功率衰落分布的差异。ETU信道中各路径的功率相对均衡，因此多径干扰明显；EPA信道中主要能量集中在首径，信号衰落相对平缓；而EVA信道中部分路径功率较强，但延迟分布较宽，导致频率选择性衰落明显。这些差异直接决定了OFDM系统在不同信道下的表现，尤其体现在信号子载波的相关性和信道估计精度上。

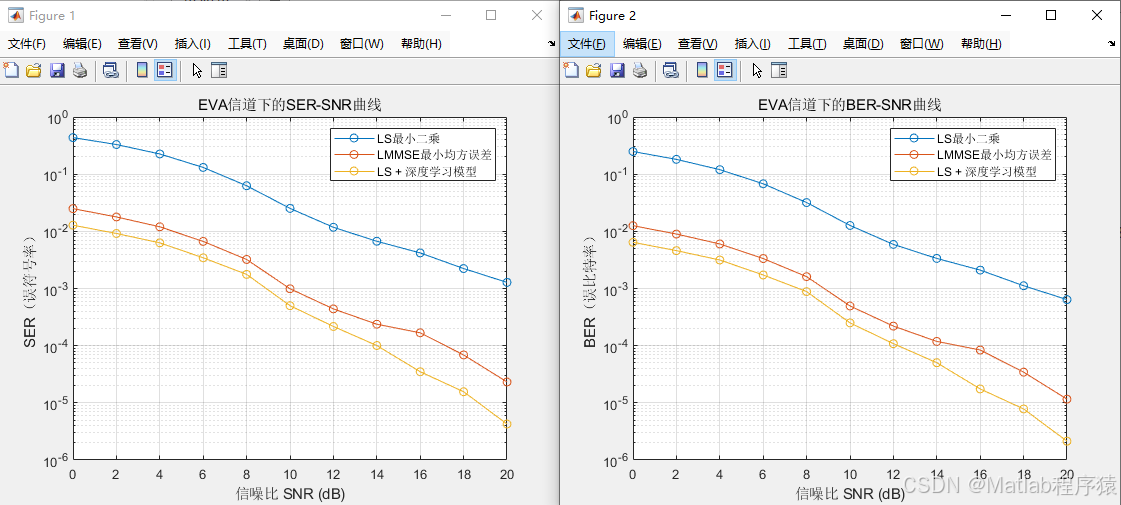
在EVA信道中，由于多径时延较长，频率响应呈现出较大的起伏，因此对导频分布和信道插值方法提出了更高要求。若导频间距过大，插值误差会导致等化后误码率显著上升；而在EPA信道中，信道变化相对平缓，导频间距可以适当增大而不影响性能；至于ETU信道，由于其强烈的多径特性和较高的多普勒扩展，系统不仅要考虑时域上的快速衰落，还需在频域上对每个子载波的增益变化进行更精细的跟踪。在这三种模型下，OFDM系统的抗衰落能力体现出明显差异：在EPA信道中，系统几乎可以近似视为平坦衰落，误比特率曲线随SNR提升迅速下降；在EVA信道中，虽然整体性能较好，但在中等信噪比区间仍会出现一定的误码地板；而在ETU信道中，若信道估计不够精确，误码率往往在较高SNR时仍无法完全收敛。

信道估计是OFDM接收端恢复数据的关键环节。理想情况下，接收端应准确获得每个子载波的复数增益以实现最优均衡。然而在实际系统中，信道状态信息无法直接获取，因此必须通过导频符号和估计算法间接恢复。最简单的一种方法是最小二乘（LS）估计，其思想是利用接收到的导频符号与已知的发送导频比值来估计信道响应。这种方法实现简单、计算量低，但缺点是对噪声非常敏感，尤其在低信噪比时估计误差较大。LS估计本质上并未利用信道的统计特性，只是对每个导频点进行直接除法操作，因此在信道平滑性较好的EPA模型中仍可获得不错结果，而在EVA或ETU这类快速衰落信道中误差明显放大。

相比之下，LMMSE（线性最小均方误差）估计在LS基础上引入了信道统计特征和噪声方差信息，通过加权优化使得估计结果在均方意义下最优。这种算法能在噪声较强或多径较多的环境中有效抑制估计误差。LMMSE通过平衡信号能量与噪声能量来修正LS估计值，从而在EVA与ETU信道下表现出更稳定的性能。尤其在中高信噪比时，LMMSE估计能显著降低误比特率，使系统的误码曲线在高SNR区间更接近理想理论值。然而LMMSE的缺点是需要知道噪声方差和信道协方差矩阵，这在动态环境中往往难以准确获得，因此在实际硬件实现中常采用近似化或简化模型来降低计算复杂度。

随着深度学习技术在通信领域的应用，第三种方式——基于神经网络的信道估计或符号判决逐渐成为研究热点。在该系统中，深度学习模型以LS估计结果或均衡后的符号作为输入，通过大量离线训练学习出信道噪声与非线性失真的隐含规律，从而对符号进行再判决或校正。模型的实质是将传统的确定性估计方法转化为数据驱动的映射关系，使得网络能够在不同信道条件下自动调整判决边界。相较于传统的LMMSE方法，深度学习模型不依赖精确的噪声方差信息，而是通过训练数据直接学习到最优映射。在EPA信道这种较为平稳的环境中，深度学习模型的优势不太明显，但在EVA与ETU这类复杂环境下，它能够捕捉非线性失真与多径叠加特征，使得符号判决更加稳健。

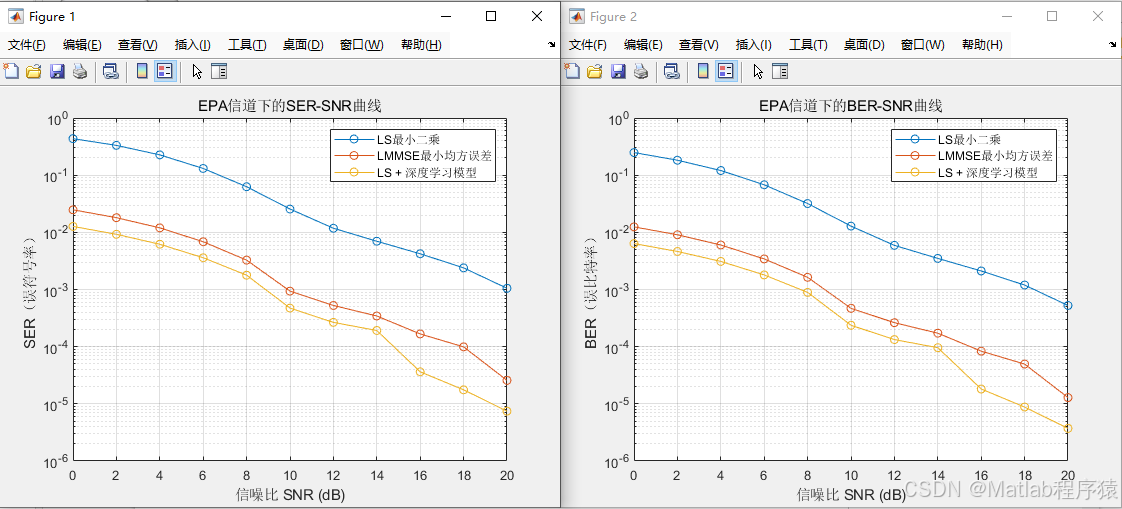
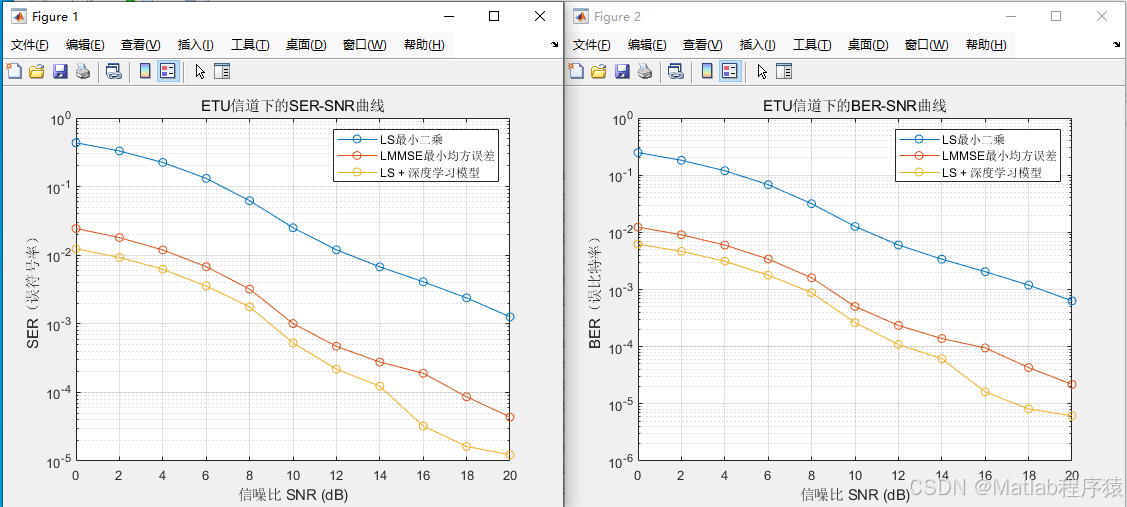
在综合比较三种信道与三种估计方式时，可以观察到明显的对应关系。对于EPA信道，由于信道平坦且变化缓慢，最简单的LS估计即可获得良好性能，此时引入LMMSE或深度学习模型的提升有限。对于EVA信道，LS估计的误差较大，LMMSE能显著改善，而深度学习进一步利用非线性特征实现更优的误码率表现。在ETU信道下，信道快速变化且多径严重，传统线性估计已难以完全应对，深度学习方法凭借模型的拟合能力，能够在高维空间中逼近真实信道响应，从而在低信噪比区域表现出比LMMSE更平滑的误码曲线。这种差异不仅体现在平均误比特率上，也体现在误码率曲线的下降趋势与收敛速度上。

在系统仿真中可以看到，随着信噪比提高，三种算法的差距逐渐缩小，这是因为高SNR下噪声对估计误差的影响减弱。LS估计虽然在低SNR时误差较大，但当噪声足够小时，三种估计方式都能接近理想性能。然而在实际应用中，多数无线通信系统工作在中低SNR区间，此时信道估计的精度尤为关键，因此LMMSE与深度学习模型的优势得以体现。从算法复杂度角度看，LS实现最简单，计算开销小，适用于实时性要求高的系统；LMMSE需要矩阵运算与噪声估计，复杂度中等；深度学习模型需经过离线训练与在线推理，虽然实时阶段计算速度较快，但模型训练成本较高。这三种方案在硬件实现中的取舍，往往取决于系统的目标性能与资源约束。

从物理层信号恢复的角度看，OFDM系统的设计本身就是为了对抗多径干扰与频率选择性衰落。通过在每个子载波上施加独立调制，系统将原本的宽带衰落信道分解为若干窄带子信道，从而简化均衡操作。然而这一特性也意味着系统对信道估计的依赖更为明显，因为每个子载波的增益都可能不同。如果估计不准，误差会在频域传播至多个符号，导致串扰效应。在EPA信道下，这种问题不严重，但在EVA与ETU环境中，插值精度与估计算法的鲁棒性成为关键。LMMSE和深度学习方案的改进，本质上都是为了在频域插值和噪声建模上取得更高的拟合精度，使得等化器输出的星座点分布更加集中，从而降低误判率。

从系统整体性能来看，三种信道环境对应着从理想到复杂再到极端的传播条件，而三种信道估计方式则体现了从简单到复杂的演进思路。LS估计在理想平稳信道下几乎无需改进即可工作；LMMSE在复杂信道中能通过统计优化弥补噪声影响；深度学习则超越传统线性框架，通过数据驱动的方法适应非理想、非高斯的信道特性。这种发展路径反映了无线通信从解析模型走向智能感知的趋势，也体现了未来系统在算法自适应与环境学习方面的潜力。

2、仿真结果演示

3、关键代码展示

略

4、MATLAB 源码获取

  V

点击下方名片关注公众号获取