强化学习之理论基础
强化学习(Reinforcement Learning, RL)是机器学习的一个分支,核心目标是让智能体(Agent)在与环境(Environment)的交互中学习最优行为策略(Policy),以最大化累积奖励(Cumulative Reward)。表示从状态 s 出发遵循策略 π 的累积奖励期望。表示在状态 s 执行动作 a 后遵循策略 π 的累积奖励期望。二者联系:解释:状态价值是所有可能动作
强化学习(Reinforcement Learning, RL)是机器学习的一个分支,核心目标是让智能体(Agent)在与环境(Environment)的交互中学习最优行为策略(Policy),以最大化累积奖励(Cumulative Reward)。
一、核心概念:构建RL问题的数学模型
1. 马尔可夫决策过程(MDP)
- 定义:强化学习的理论基石,用五元组 (S, A, P, R, γ) 描述环境:
- S:状态空间(State Space),表示环境所有可能的状态(如棋盘局面、游戏画面)。
- A:动作空间(Action Space),表示智能体可执行的动作集合(如移动方向、攻击技能)。
- P:状态转移概率(Transition Probability),P(s'|s,a) 表示在状态 s 执行动作 a 后转移到 s' 的概率。
- R:奖励函数(Reward Function),R(s,a,s') 表示状态转移后的即时奖励(如得分、惩罚)。
- γ:折扣因子(Discount Factor),取值范围 [0,1],控制未来奖励的权重(γ=0 仅关注即时奖励,γ=1 平等看待所有奖励)。
- 作用:通过MDP建模,将现实问题抽象为数学可解的形式,使智能体能够基于概率和奖励进行决策。
2. 策略与价值函数
- 策略(Policy):智能体的行为准则,分为:
- 确定性策略:π(s) = a,直接给出状态 s 下的最优动作。
- 随机性策略:π(a|s),输出动作的概率分布(如探索时随机选择)。
- 价值函数:衡量状态或动作的长期收益:
- 状态价值函数:
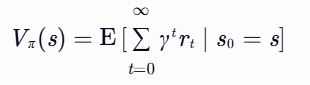
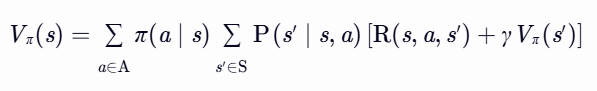
表示从状态 s 出发遵循策略 π 的累积奖励期望。
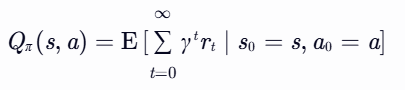
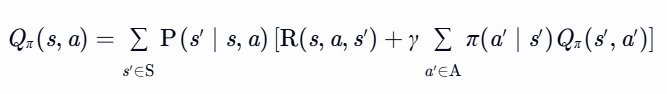
表示在状态 s 执行动作 a 后遵循策略 π 的累积奖励期望。
- 关系:价值函数为策略优化提供依据,最优策略 π* 满足 π*(s) = argmax_a Q_π*(s,a)。
二者联系:
- 从Qπ 到 Vπ:
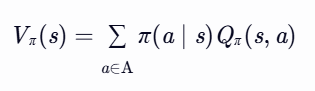
解释:状态价值是所有可能动作价值的期望(按策略 π 加权)。
- 从Vπ 到 Qπ:
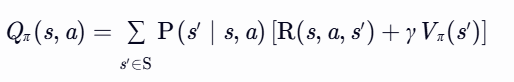
解释:动作价值由即时奖励和下一状态的折扣价值组成(后续动作仍由 π 决定)。
3. 探索与利用(Exploration vs. Exploitation)
- 定义:
- 探索:尝试未知动作,发现潜在高奖励行为。
- 利用:选择已知最优动作,最大化当前收益。
- 平衡方法:
- ε-贪心策略:以概率 ε 随机探索,1-ε 选择当前最优动作。
- Softmax策略:基于动作价值函数概率选择,高价值动作概率更高。
ε-贪心策略
数学表达
给定动作价值函数 Q(s,a)(表示在状态 s 下执行动作 a 的预期累积回报),策略定义为:

其中,|A(s)|表示在状态s下的动作数量,ε是一个介于0到1之间的数。
优点
- 简单高效:实现直观,计算复杂度低,适用于大规模动作空间。
- 保证探索:无论动作价值估计如何,始终以固定概率探索未知动作。
缺点
- 探索效率低:对所有非最优动作一视同仁,可能导致无效探索(如高方差动作被过度尝试)。
- 缺乏适应性:ε为固定值时,无法根据动作价值的差异动态调整探索强度。
Softmax策略
核心思想
- 基于价值概率选择:动作被选中的概率与其价值函数值成指数正相关(通过Softmax函数计算)。
- 温度参数控制:通过超参数 τ(温度) 调节探索强度:
- 高τ:动作概率分布更均匀(鼓励探索)。
- 低τ:动作概率分布更集中于高价值动作(鼓励利用)。
数学表达
动作选择概率为:
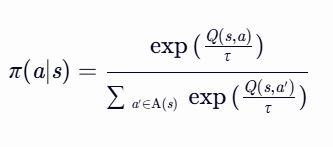
- 解释:
- 指数化价值:通过 exp(Q(s,a)/τ) 将价值映射为非负概率权重。
- 归一化:分母为所有动作的权重和,确保概率总和为1。
优点
- 自适应探索:动作价值差异越大,高价值动作被选中的概率越高,低价值动作被逐步淘汰。
- 平滑过渡:通过温度参数 τ 动态平衡探索与利用,避免ε-贪心的“硬切换”。
缺点
- 计算复杂度高:需对所有动作计算指数函数,在大规模动作空间中效率较低。
- 超参数敏感:τ 的选择需结合任务特性,过高导致无效探索,过低导致过早收敛。
二、理论框架:动态规划与最优控制
动态规划(Dynamic Programming, DP)和最优控制理论是强化学习求解马尔可夫决策过程(MDP)的核心方法,通过递归分解和迭代优化求解最优策略。
1、贝尔曼方程(Bellman Equation)
1)核心定义
贝尔曼方程将价值函数的求解分解为即时奖励与未来价值的递归关系,分为两类:
- 贝尔曼期望方程(用于策略评估)
描述在给定策略 π 下,价值函数 Vπ(s) 和 Qπ(s,a) 的递归关系:
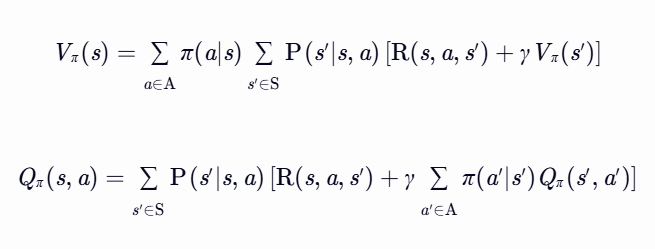
- 作用:评估当前策略的优劣,用于策略迭代中的策略评估步骤。
- 贝尔曼最优方程(用于策略优化)
描述最优价值函数 V∗(s) 和 Q∗(s,a) 的递归关系:
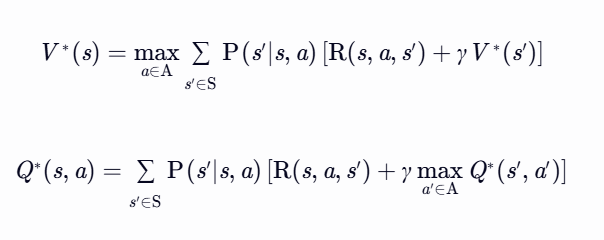
- 作用:求解最优策略,用于值迭代或策略改进步骤。
2、动态规划方法(DP)
动态规划基于贝尔曼方程,通过迭代更新价值函数或策略求解MDP,分为策略迭代和值迭代两类方法。
1)策略迭代(Policy Iteration)
流程:
策略评估(Policy Evaluation)
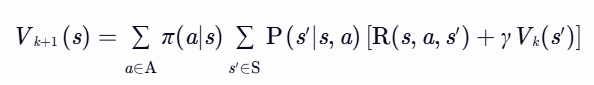
终止条件:∥Vk+1−Vk∥∞<θ(θ 为预设阈值)。
策略改进(Policy Improvement)
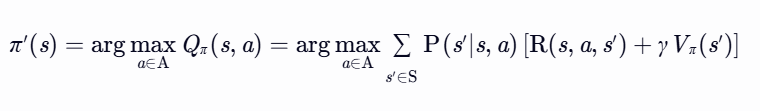
终止条件:若 π′=π,则 π 为最优策略。
收敛性:策略迭代保证在有限步内收敛至最优策略(因策略空间有限)。
2)值迭代(Value Iteration)
流程:
直接优化价值函数
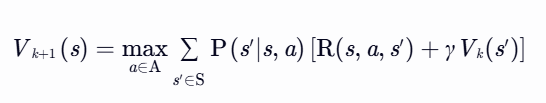
终止条件:∥Vk+1−Vk∥∞<θ
策略提取(Policy Extraction)
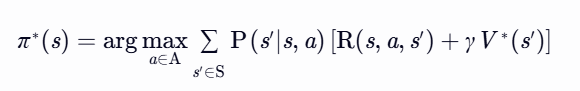
收敛性: 值迭代保证收敛至最优价值函数 V∗,且迭代次数与 γ 和状态空间大小相关。
3)策略迭代 vs值迭代
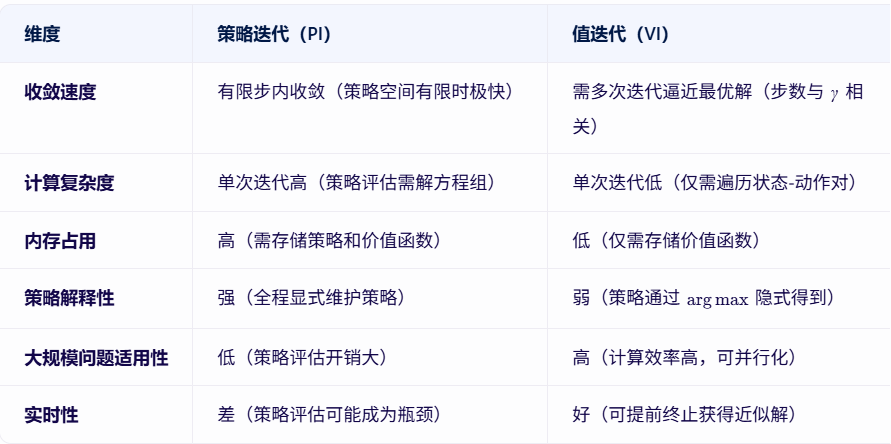
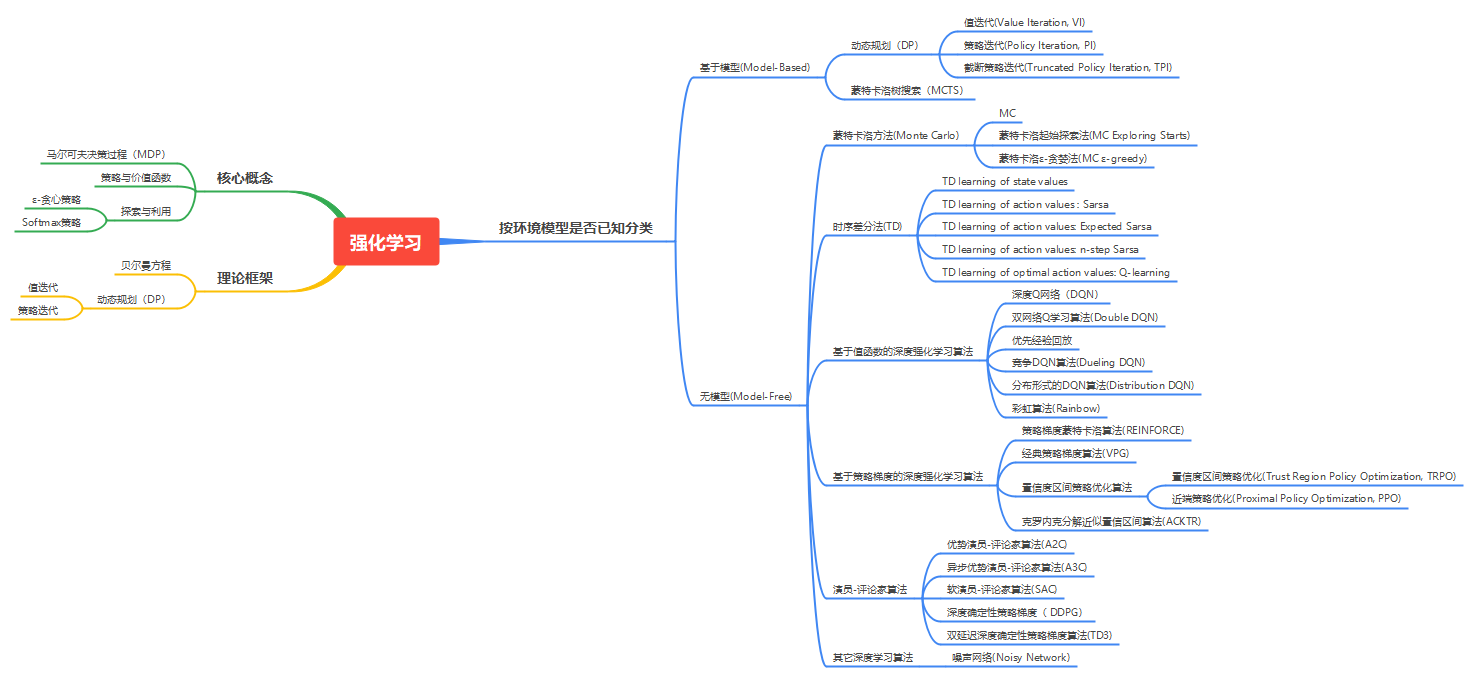
三、强化学习的分类
1、基于模型的(Model-Based)和无模型的(Model-Free)
强化学习(RL)的核心目标是让智能体(Agent)通过与环境的交互学习最优策略。根据是否依赖对环境的显式建模,RL方法可分为基于模型(Model-Based)和无模型(Model-Free)两大类。
基于模型(Model-Based)强化学习
- 定义:智能体通过学习或预定义的方式,显式构建环境的动态模型(即状态转移函数 P(s′∣s,a) 和奖励函数 R(s,a,s′)),并利用该模型进行策略优化。(先学习规则,再行动)
- 学习过程:
- 模型学习:通过交互数据拟合环境动态(如神经网络预测 s′ 和 r)。
- 规划(Planning):利用模型在虚拟环境中模拟多种策略(如蒙特卡洛树搜索MCTS、动态规划)。
- 策略执行:将最优策略部署到真实环境。
- 优缺点:

无模型(Model-Free)强化学习
- 定义:智能体不显式建模环境动态,而是直接通过与真实环境的交互数据(如状态、动作、奖励)学习策略或价值函数。(直接行动,边行动边学习规则)
- 学习过程:
- 直接试错:通过实际交互数据更新策略(如Q-Learning)或价值函数(如SARSA)。
- 无需虚拟模拟:所有学习依赖真实反馈,无中间模型。
- 优缺点:
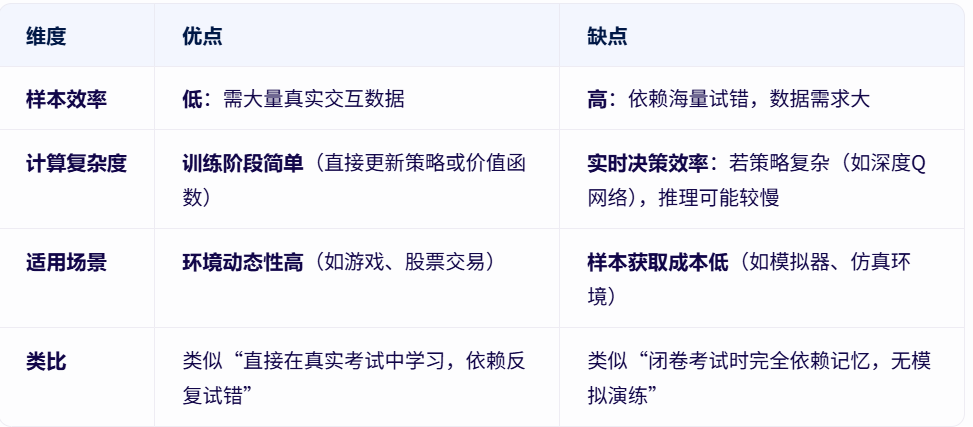
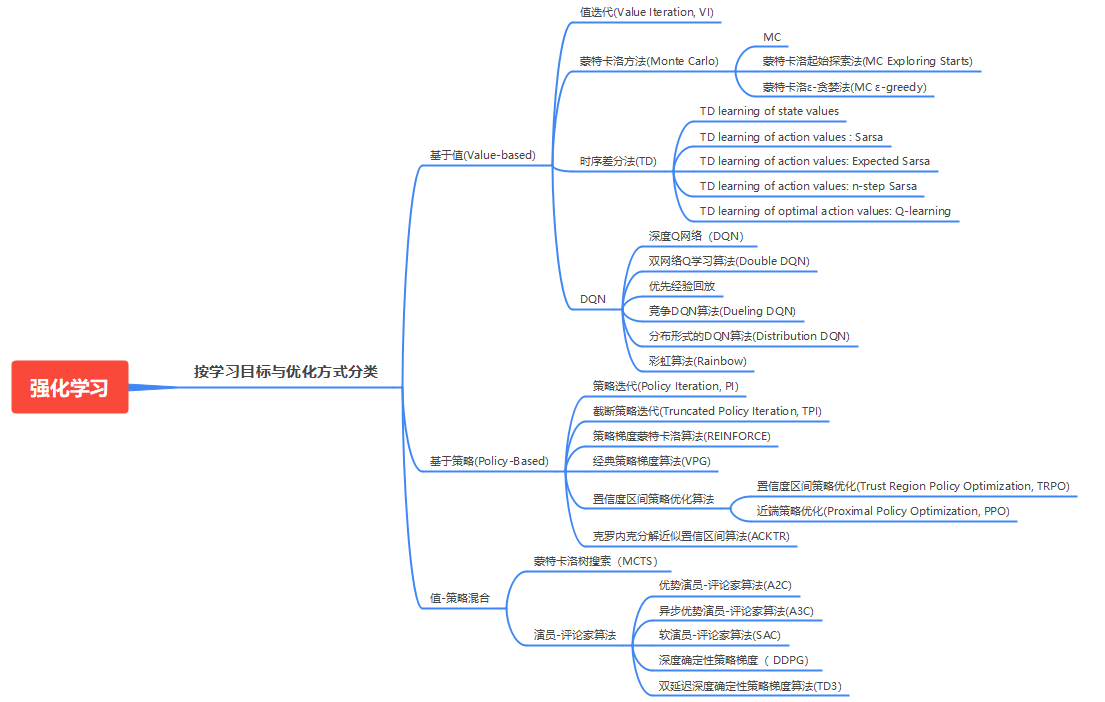
2、基于策略(Policy-Based)的和基于价值的(Value-Based)
根据学习方式的不同,RL算法可分为基于策略(Policy-Based)和基于价值(Value-Based)两大类。
基于策略(Policy-Based)强化学习
- 定义:直接学习策略函数 πθ(a∣s),即给定状态 s 时选择动作 a 的概率分布(参数为 θ)。策略的优化目标是最小化/最大化累积奖励的期望(如梯度上升)。
- 关键公式:
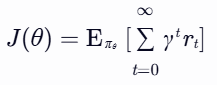
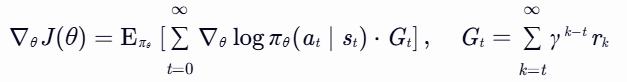
沿累积奖励 Gt 的方向调整策略参数θ,使高奖励动作的概率增加。
- 优缺点:
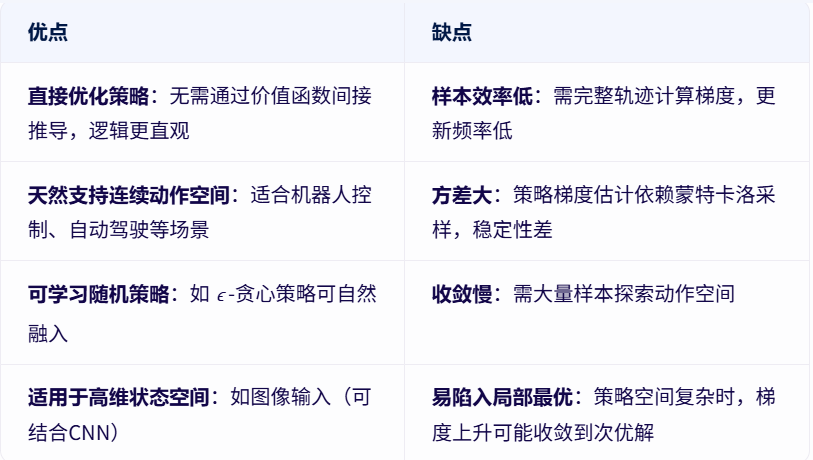
基于价值(Value-Based)强化学习
- 定义:学习价值函数(如状态价值 Vπ(s) 或动作价值 Qπ(s,a)),并通过价值函数间接推导策略(如选择价值最高的动作)。
- 关键公式:
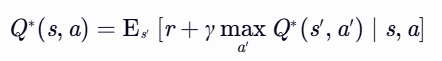
- 策略提取:
![]()
直接选择当前状态下价值最大的动作,无需显式学习策略函数。
- 优缺点:

基于策略VS基于价值
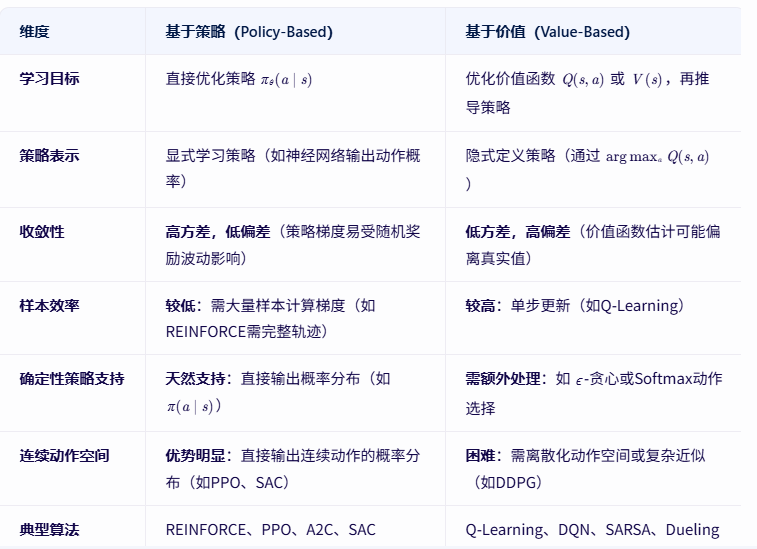
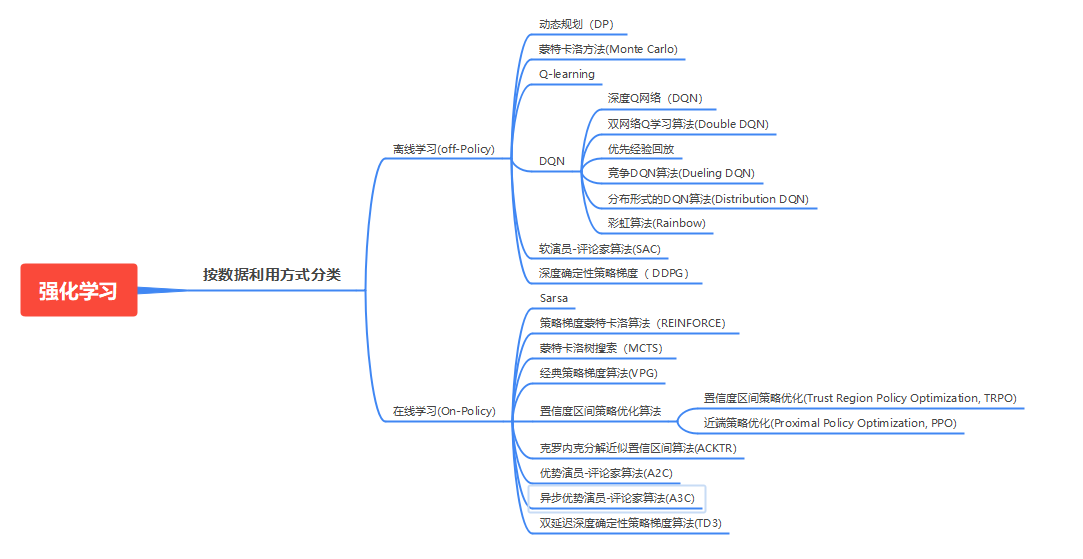
3、在线(On-policy)和离线(Off-policy)学习
根据数据使用方式的不同,RL算法可分为在线(On-policy)和离线(Off-policy)两类。
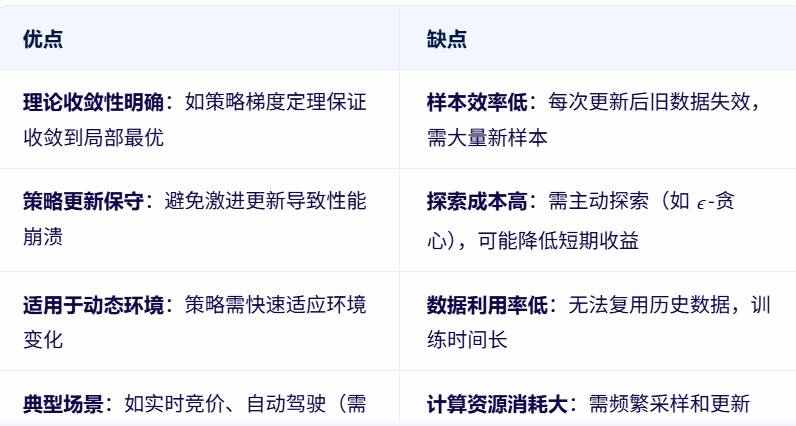
在线(On-policy)学习
- 定义:智能体使用当前策略生成的经验数据来更新策略本身。即“边学习边实践”,数据与策略同步更新。
- 优缺点:
离线(Off-policy)学习
- 定义:智能体使用历史策略(或任意策略)生成的经验数据来更新当前策略。即“用旧数据指导新策略”,数据与策略解耦。
- 优缺点:

混合方法
- 重要性采样(Importance Sampling):
- 问题:离线数据与当前策略分布不匹配。
- 解决:通过重要性权重调整梯度(如PPO的剪切约束隐式处理分布偏移)。
- 经验回放(Experience Replay):
- 典型算法:DQN、DDPG、SAC。
- 优势:将历史数据存入缓冲区,随机采样更新,打破数据相关性。
- Actor-Critic架构:
- 在线策略梯度(Actor):保证策略稳定更新。
- 离线价值估计(Critic):利用历史数据高效学习价值函数。
- 典型算法:A2C(在线Critic)、SAC(离线Critic + 最大熵RL)。
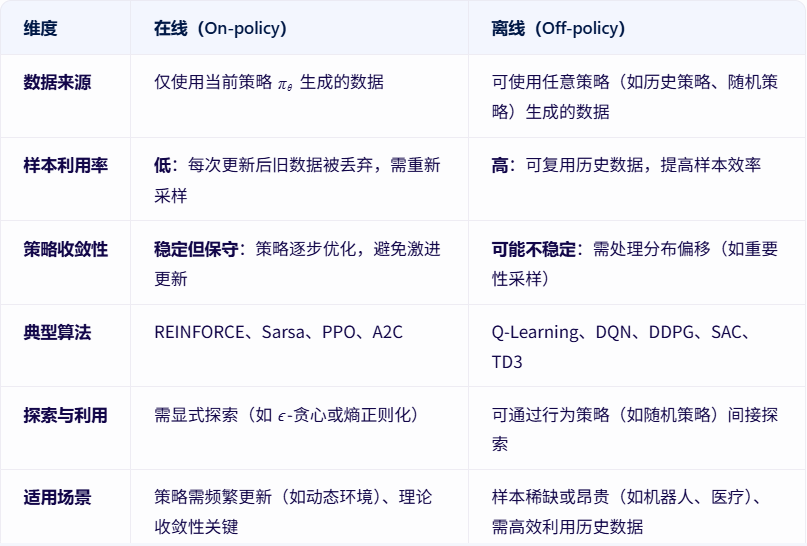
在线VS离线
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容






所有评论(0)