对数在深度学习中的三个超重要作用(含代码示例)
| 连乘变连加| $\log(ab) = \log a + \log b$ | 提高数值稳定性(如概率乘积)|| 指数拉下来| $\log(e^x) = x$| 简化导数计算,稳定梯度传播|| 缩放可视化范围 | `plt.yscale('log')`| loss/梯度大范围可视化,清晰展示变化 |
对数在深度学习中的三个超重要作用(含代码示例)
在深度学习中,“对数(log)”是一个非常常见的数学工具。你可能经常会在交叉熵损失函数、softmax 函数、负对数似然等地方看到它的身影。
今天我们就来聊聊,对数函数到底在深度学习中起到了什么作用?为什么它如此重要?
✨ 作用一:把“连乘”变成“连加”——让运算更简单、更稳定!
在数学中,有一个很重要的对数恒等式:
log(ab)=loga+logb \log(ab) = \log a + \log b log(ab)=loga+logb
这个性质可以推广到多个数相乘的情形:
log(a⋅b⋅c⋯z)=loga+logb+logc+⋯+logz \log(a \cdot b \cdot c \cdots z) = \log a + \log b + \log c + \cdots + \log z log(a⋅b⋅c⋯z)=loga+logb+logc+⋯+logz
✅ 举个例子:
假设我们有一组小概率值:
p1=0.001,p2=0.002,p3=0.0005 p_1 = 0.001,\quad p_2 = 0.002,\quad p_3 = 0.0005 p1=0.001,p2=0.002,p3=0.0005
我们想要计算这些概率的乘积:
p=p1⋅p2⋅p3=0.001⋅0.002⋅0.0005=1×10−9 p = p_1 \cdot p_2 \cdot p_3 = 0.001 \cdot 0.002 \cdot 0.0005 = 1 \times 10^{-9} p=p1⋅p2⋅p3=0.001⋅0.002⋅0.0005=1×10−9
这个数非常小,可能会导致浮点数下溢问题(在计算机中表现为精度损失或变成0)。
🧠 怎么办?我们用对数转换!
log(p)=log(p1)+log(p2)+log(p3) \log(p) = \log(p_1) + \log(p_2) + \log(p_3) log(p)=log(p1)+log(p2)+log(p3)
我们用自然对数(ln)来计算:
log(0.001)≈−6.9,log(0.002)≈−6.2,log(0.0005)≈−7.6 \log(0.001) ≈ -6.9,\quad \log(0.002) ≈ -6.2,\quad \log(0.0005) ≈ -7.6 log(0.001)≈−6.9,log(0.002)≈−6.2,log(0.0005)≈−7.6
相加:
log(p)≈−6.9−6.2−7.6=−20.7 \log(p) ≈ -6.9 - 6.2 - 7.6 = -20.7 log(p)≈−6.9−6.2−7.6=−20.7
现在就不会出现“太小乘太小等于0”的问题了,稳定性大大提高!
🤖 对数在深度学习中的典型应用场景:
-
语言模型中的概率计算:在预测一句话时,需要将每个词的生成概率相乘,得到整句话的联合概率。由于这些概率通常非常小,直接相乘容易造成数值下溢。使用对数后,乘积变为加法,避免精度问题,且便于计算:
log(p1⋅p2⋅⋯⋅pn)=logp1+logp2+⋯+logpn \log(p_1 \cdot p_2 \cdot \cdots \cdot p_n) = \log p_1 + \log p_2 + \cdots + \log p_n log(p1⋅p2⋅⋯⋅pn)=logp1+logp2+⋯+logpn
-
最大似然估计(MLE):MLE 的目标是最大化所有样本的似然函数(概率乘积)。取对数后变成 log-likelihood,即对 log 概率求和,转化为更容易优化的加法形式:
max∏ip(xi)⇒max∑ilogp(xi) \max \prod_i p(x_i) \quad \Rightarrow \quad \max \sum_i \log p(x_i) maxi∏p(xi)⇒maxi∑logp(xi)
✨ 作用二:把“指数”拉下来 —— 简化梯度求导
对数另一个重要恒等式:
log(ex)=x \log(e^x) = x log(ex)=x
这让我们可以将 指数函数“拉”下来,方便求导与优化。
✅ 举例:交叉熵损失中的 softmax
Softmax 定义:
softmax(xi)=exi∑jexj \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} softmax(xi)=∑jexjexi
交叉熵损失函数:
CrossEntropy=−∑iyilog(softmax(xi)) \text{CrossEntropy} = -\sum_i y_i \log(\text{softmax}(x_i)) CrossEntropy=−i∑yilog(softmax(xi))
如果没有 log,这个函数在反向传播时梯度非常复杂。加上 log 后:
- 分子里的 exie^{x_i}exi 被 log 拉下来;
- 大量指数项互相抵消;
- 梯度计算稳定、效率高。
🧠 应用场景:
- 分类模型中的损失函数(如 cross entropy);
- softmax 输出求导;
- 负对数似然损失(NLLLoss)。
🌟 为什么说 “交叉熵本质上是在 softmax 上加了 log”?
📌 背景设定:分类任务
假设一个图像分类模型,最后输出的 logits 是(未归一化的得分):
z = [2.0, 1.0, 0.1] # 猫 狗 鸟
🧮 第一步:softmax 把 logits 变成概率
softmax 会对这些 logits 做指数变换 + 归一化:
y^i=ezi∑jezj \hat{y}_i = \frac{e^{z_i}}{\sum_j e^{z_j}} y^i=∑jezjezi
假设计算后得到:
softmax 输出 = [0.7, 0.2, 0.1]
- 猫的概率是 0.7
- 狗是 0.2
- 鸟是 0.1
这就变成了模型对每个类别的“信心”。
🧮 第二步:交叉熵损失计算
假设真实标签是“猫”,我们用 one-hot 表示为:
y = [1, 0, 0]
交叉熵定义是:
CrossEntropy(y,y^)=−∑iyilog(y^i) \text{CrossEntropy}(y, \hat{y}) = -\sum_i y_i \log(\hat{y}_i) CrossEntropy(y,y^)=−i∑yilog(y^i)
因为只有 y0=1y_0 = 1y0=1,其他为 0,所以其实只保留一项:
CrossEntropy=−log(y^0)=−log(0.7) \text{CrossEntropy} = -\log(\hat{y}_0) = -\log(0.7) CrossEntropy=−log(y^0)=−log(0.7)
这个计算就等价于:
交叉熵 = 对正确类别的预测概率,取负对数
所以我们说:
交叉熵只是在 softmax 输出的概率上,加了一个
-log操作(只对正确的那个类别)。
🔁 为什么这么做有意义?
让我们看 log 的图像来理解这个惩罚机制:
| 预测概率 y^\hat{y}y^ | −log(y^)-\log(\hat{y})−log(y^) |
|---|---|
| 1.0 | 0.0 (完美预测) |
| 0.9 | ~0.1 |
| 0.5 | ~0.69 |
| 0.1 | ~2.30 |
| 0.01 | ~4.60 |
- 预测越准,损失越小
- 预测错得越离谱,损失越大
这就自然形成了优化目标,让模型学会输出更接近正确标签的高概率。
🔧 补充:为什么我们说“softmax + log”
有时候在代码里(比如 torch.nn.CrossEntropyLoss),其实并不会显式地先算 softmax,再取 log,而是直接结合成一个函数叫:
👉 log_softmax
log(ezi∑jezj)=zi−log(∑jezj) \log\left(\frac{e^{z_i}}{\sum_j e^{z_j}}\right) = z_i - \log\left(\sum_j e^{z_j}\right) log(∑jezjezi)=zi−log(j∑ezj)
这样能避免数值不稳定、效率更高。因此,在底层实现中:
CrossEntropy = log_softmax + NLLLoss(负对数似然)
✅ 总结一句话
交叉熵损失就是:让正确类别的预测概率越接近 1 越好;通过对 softmax 概率取负对数来惩罚错误的预测。
✨ 作用三:绘图中使用对数坐标 —— 缩放宽幅数值范围
当我们要绘制数值跨度很大的数据时,比如 loss 从 100 降到 0.001,线性坐标下小数值部分几乎不可见。
这时,使用 对数坐标轴(log scale) 可以大大提升可视化效果。
✅ 示例代码:对比普通坐标和对数坐标
import matplotlib.pyplot as plt
import numpy as np
# 模拟一个 loss 下降过程(指数衰减)
epochs = np.arange(1, 51)
loss = 10 * np.exp(-0.2 * epochs)
plt.figure(figsize=(12, 5))
# 子图1:线性坐标
plt.subplot(1, 2, 1)
plt.plot(epochs, loss, marker='o')
plt.title('Linear Scale')
plt.xlabel('Epoch')
plt.ylabel('Loss')
# 子图2:对数坐标
plt.subplot(1, 2, 2)
plt.plot(epochs, loss, marker='o')
plt.yscale('log') # 重点:对数坐标轴
plt.title('Log Scale (Y-axis)')
plt.xlabel('Epoch')
plt.ylabel('Loss (log scale)')
plt.tight_layout()
plt.show()
🔍 效果对比:
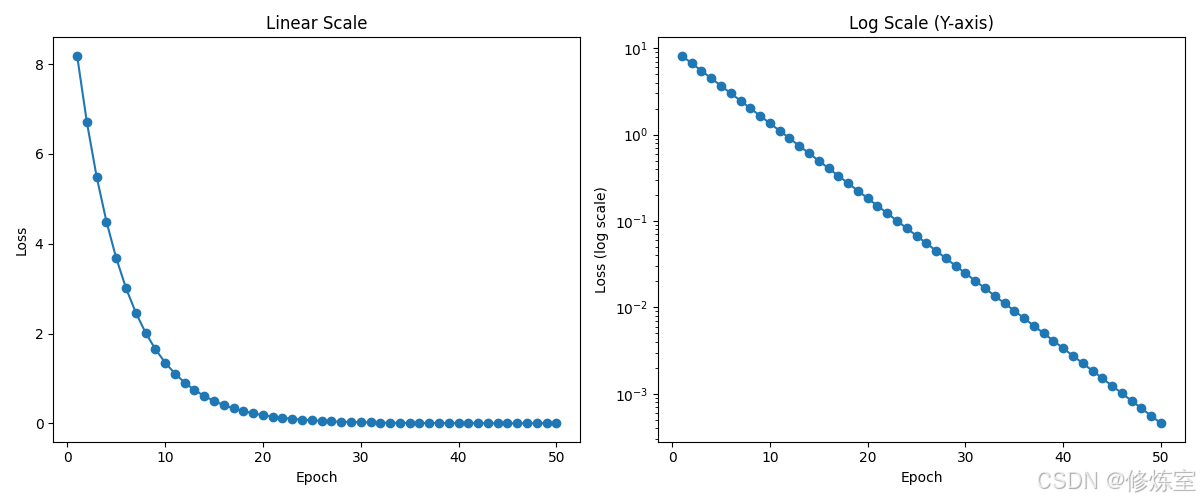
- 左图(线性坐标):后期 loss 接近 0,变化几乎看不见;
- 右图(对数坐标):每一阶段的 loss 变化都清晰可见,指数衰减在图中变成直线,更利于分析。
🧠 应用场景:
- 绘制 loss、accuracy 随 epoch 的变化(尤其是指数级别的收敛);
- 梯度值或权重分布的可视化;
- Zipf 分布、对抗攻击曲线等常见 log-log 图;
- 对数学习率(学习率搜索时 x 轴用 log)。
✅ 总结表格
| 功能 | 对数恒等式 | 实际用途 |
|---|---|---|
| 连乘变连加 | log(ab)=loga+logb\log(ab) = \log a + \log blog(ab)=loga+logb | 提高数值稳定性(如概率乘积) |
| 指数拉下来 | log(ex)=x\log(e^x) = xlog(ex)=x | 简化导数计算,稳定梯度传播 |
| 缩放可视化范围 | plt.yscale('log') |
loss/梯度大范围可视化,清晰展示变化 |
🎯 最后总结
对数(log)是深度学习中不可缺少的工具:
- log 能让损失函数凸化,使优化更容易;
- log 可以避免概率接近 0 时的数值下溢问题;
- log 简化复杂的乘法和指数操作;
- log 让你的图像更漂亮、更具可读性!
- log+softmax 是天然的组合,广泛用于分类问题;
下一次看到 log,不要慌,它是你模型背后的“隐形英雄”!
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容






所有评论(0)