手搓 自然语言模型 各种对比数据
从上面实验数据可知 在使用方案 二的时候 ,如代码写 不断的扩大维度方可提高收敛时候的acc 上限且最高。且该网络模型可以在推理的时候如最后一幅图所示可以,进行单独解码 从而节约算力。后面两幅图中 带框的两个是两个不同的方案,不带框的是公共部分。经过测试抛弃了蓝色框的方案。
·
基础模型和设计思想
最优网络结构
import paddle
import numpy as np
from tqdm import tqdm
class EmMask(paddle.nn.Layer):
def __init__(self, voc_size=19, hidden_size=256, max_len=48):
super(EmMask, self).__init__()
# 定义输入序列和标签序列
self.embedding_layer = paddle.nn.Embedding(voc_size, hidden_size)
self.pos_em_layer = paddle.nn.Embedding(max_len, hidden_size)
self.pos_to_down = paddle.nn.Linear(hidden_size, 1)
self.sample_buffer_data=paddle.zeros([1])
# 定义模型计算过程
def forward(self, x):
# 将输入序列嵌入为向量表示
embedded_x = self.embedding_layer(x) # bs--->bsh
# embedded_x += paddle.fft.fft(embedded_x, axis=1).real()
# embedded_p 有权重 后期预测的时候就要参与 这样会造成计算量增加 如果使用 1 代替 减少多样性
# 但是使用pos 是 对于任何输入是固定的可以事先弄好的可以事先计算,一个固定的w 而已
# 而当前的attention 这个参数是动态的,要通过其他方法来实现动态的 比如scale 多头等
# 当前这种方式全靠 开头和结尾 中间固定参数哦 如果使用多个 加上softmax 那么就能完成多头scale 的操作了
embedded_p = self.pos_em_layer(paddle.arange(1, x.shape[1] + 1).astype("int64"))
embedded_p = self.pos_to_down(embedded_p)
xp = embedded_x.transpose([0, 2, 1]).unsqueeze(3) @ embedded_p.transpose([1, 0])
# mask
mask = paddle.triu(paddle.ones([xp.shape[-1], xp.shape[-1]]))
x = xp * mask
return x
class JustMaskEm(paddle.nn.Layer):
def __init__(self, voc_size=19, hidden_size=512, max_len=1024):
super(JustMaskEm, self).__init__()
# 定义输入序列和标签序列
self.em_mask_one = paddle.nn.Embedding(voc_size, hidden_size)
self.em_mask_two = EmMask(voc_size, hidden_size, max_len)
self.head_layer = paddle.nn.Linear(hidden_size, voc_size,bias_attr=False)
self.layer_nor = paddle.nn.LayerNorm(hidden_size)
# 定义模型计算过程
def forward(self, x):
one = self.em_mask_one(x)
two = self.em_mask_two(x)
x = one* paddle.sum(two, -2).transpose([0,2,1])
# x = paddle.sum(x, -2)
# x=x.transpose([0, 2, 1])
# x = self.head_layer(self.layer_nor(x))
x = self.head_layer(self.layer_nor(x))
return x
# 进行模型训练和预测
# if __name__ == '__main__':
# net = JustMaskEm()
# X = paddle.to_tensor([
# [1, 2, 3, 4],
# [5, 6, 7, 8]
# ], dtype='int64')
# print(net(X).shape)
# print(net.sample_buffer(X).shape)
#
def train_data():
net = JustMaskEm(voc_size=len(voc_id))
net.load_dict(paddle.load("long_attention_model"))
print("加载成功")
opt = paddle.optimizer.Adam(parameters=net.parameters(), learning_rate=0.0003)
loss_f = paddle.nn.CrossEntropyLoss()
loss_avg = []
acc_avg = []
batch_size = 1000*3
bar=tqdm(range(1, 3 * 600))
for epoch in bar:
np.random.shuffle(data_set)
for i, j in [[i, i + batch_size] for i in range(0, len(data_set), batch_size)]:
one_data = data_set[i:j]
if (len(acc_avg) + 1) % 1000 == 0:
# print(np.mean(loss_avg), "____", np.mean(acc_avg))
paddle.save(net.state_dict(), "long_attention_model")
paddle.save({"data": loss_avg}, "loss_avg")
paddle.save({"data": acc_avg}, "acc_avg")
one_data = paddle.to_tensor(one_data)
in_put = one_data[:, :-1]
label = one_data[:, 1:]
# label = one_data[:, 1:]
out = net(in_put)
loss = loss_f(out.reshape([-1, out.shape[-1]]), label.reshape([-1]).astype("int64"))
acc = np.mean((paddle.argmax(out, -1)[:, :].reshape([-1]) == label[:, :].reshape([-1])).numpy())
# loss = loss_f(out, label.reshape([-1]).astype("int64"))
# acc = np.mean((paddle.argmax(out, -1) == label.reshape([-1])).numpy())
loss_data = loss.numpy()[0]
acc_avg.append(acc)
loss_avg.append(loss_data)
bar.set_description(desc="{}{}{}{}{}".format(epoch, "____", np.mean(loss_avg), "____", np.mean(acc_avg)))
opt.clear_grad()
loss.backward()
opt.step()
if np.mean(acc_avg) > 0.80:
opt.set_lr(opt.get_lr() / (np.mean(acc_avg) * 100 + 1))
print(np.mean(loss_avg), "____", np.mean(acc_avg))
paddle.save(net.state_dict(), "long_attention_model")
paddle.save({"data": loss_avg}, "loss_avg")
paddle.save({"data": acc_avg}, "acc_avg")
if __name__ == "__main__":
with open("poetrySong.txt", "r", encoding="utf-8") as f:
data1 = f.readlines()
data1 = [i.strip().split("::")[-1] for i in data1 if len(i.strip().split("::")[-1]) == 32]
voc_id = ["sos"] + sorted(set(np.hstack([list(set(list("".join(i.split())))) for i in data1]))) + ["pad"]
data_set = [[voc_id.index(j) for j in i] for i in data1]
train_data()
实验对比数据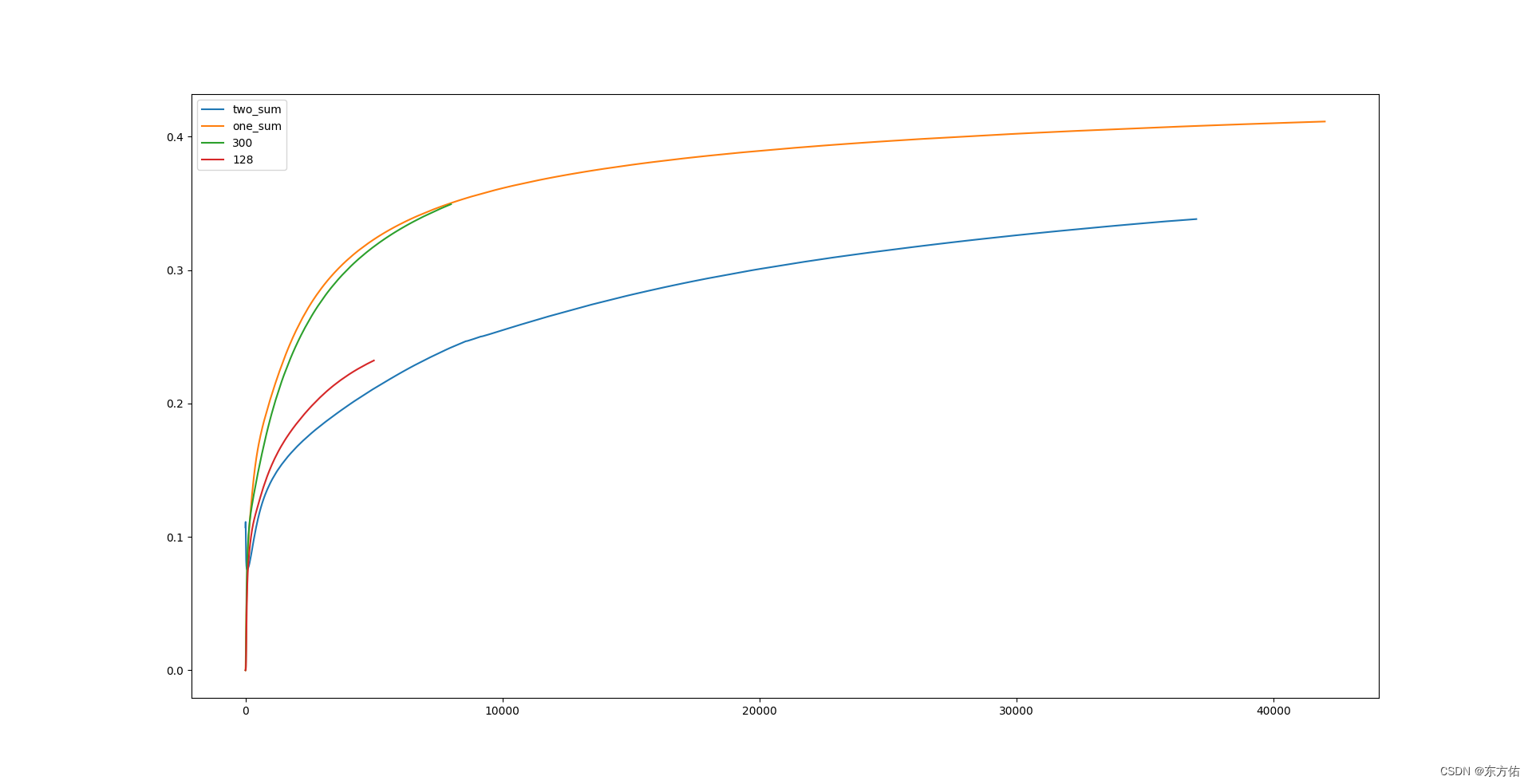
两种基本网络结构设计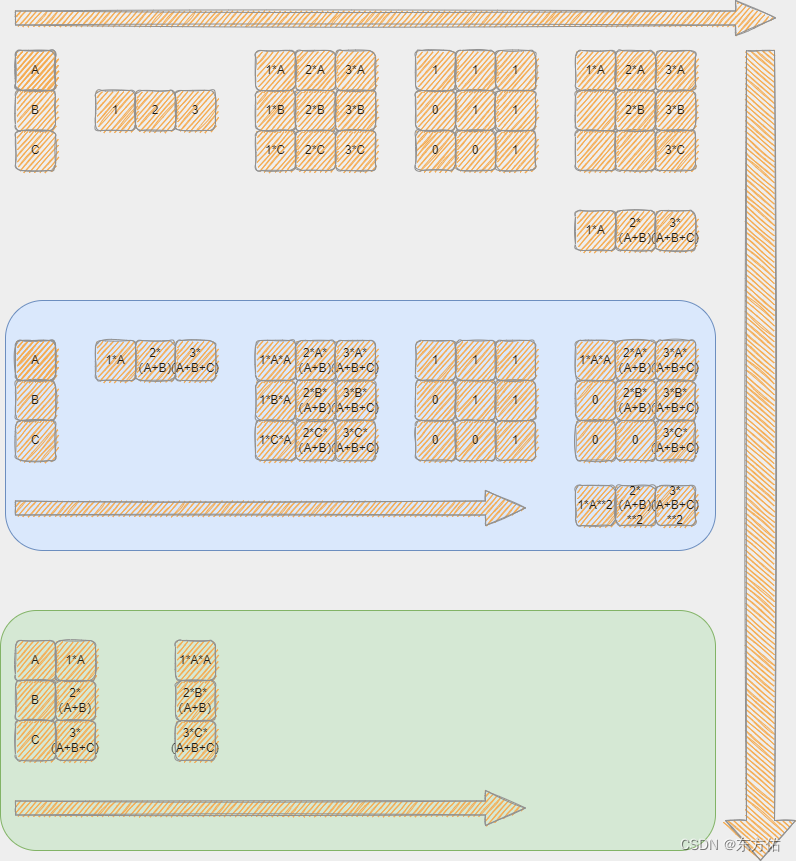
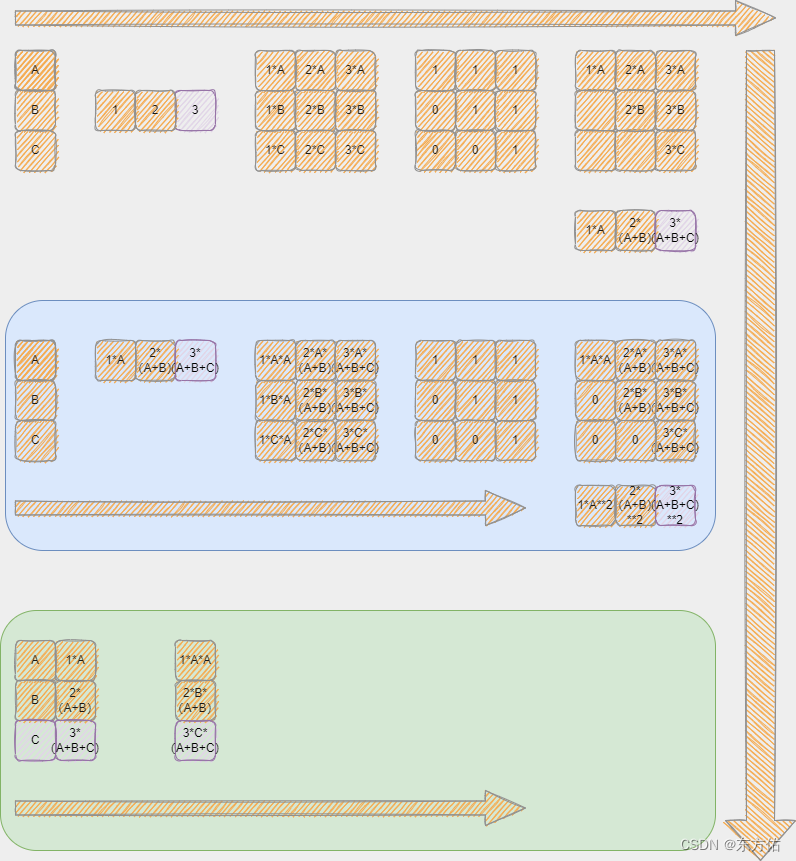
推理
import paddle
import numpy as np
from tqdm import tqdm
class EmMask(paddle.nn.Layer):
def __init__(self, voc_size=19, hidden_size=256, max_len=48):
super(EmMask, self).__init__()
# 定义输入序列和标签序列
self.embedding_layer = paddle.nn.Embedding(voc_size, hidden_size)
self.pos_em_layer = paddle.nn.Embedding(max_len, hidden_size)
self.pos_to_down = paddle.nn.Linear(hidden_size, 1)
self.sample_buffer_data=paddle.zeros([1])
# 定义模型计算过程
def forward(self, x):
# 将输入序列嵌入为向量表示
embedded_x = self.embedding_layer(x) # bs--->bsh
# embedded_x += paddle.fft.fft(embedded_x, axis=1).real()
# embedded_p 有权重 后期预测的时候就要参与 这样会造成计算量增加 如果使用 1 代替 减少多样性
# 但是使用pos 是 对于任何输入是固定的可以事先弄好的可以事先计算,一个固定的w 而已
# 而当前的attention 这个参数是动态的,要通过其他方法来实现动态的 比如scale 多头等
# 当前这种方式全靠 开头和结尾 中间固定参数哦 如果使用多个 加上softmax 那么就能完成多头scale 的操作了
embedded_p = self.pos_em_layer(paddle.arange(1, x.shape[1] + 1).astype("int64"))
embedded_p = self.pos_to_down(embedded_p)
xp = embedded_x.transpose([0, 2, 1]).unsqueeze(3) @ embedded_p.transpose([1, 0])
# mask
mask = paddle.triu(paddle.ones([xp.shape[-1], xp.shape[-1]]))
x = xp * mask
return x
def sample(self, x):
# 将输入序列嵌入为向量表示
embedded_x = self.embedding_layer(x) # bs--->bsh
# embedded_x += paddle.fft.fft(embedded_x, axis=1).real()
# embedded_p 有权重 后期预测的时候就要参与 这样会造成计算量增加 如果使用 1 代替 减少多样性
# 但是使用pos 是 对于任何输入是固定的可以事先弄好的可以事先计算,一个固定的w 而已
# 而当前的attention 这个参数是动态的,要通过其他方法来实现动态的 比如scale 多头等
# 当前这种方式全靠 开头和结尾 中间固定参数哦 如果使用多个 加上softmax 那么就能完成多头scale 的操作了
embedded_p = self.pos_em_layer(paddle.arange(x.shape[1], x.shape[1] + 1).astype("int64"))
embedded_p = self.pos_to_down(embedded_p)
xp = paddle.sum(embedded_x,1)*embedded_p
return xp
class JustMaskEm(paddle.nn.Layer):
def __init__(self, voc_size=19, hidden_size=512, max_len=1024):
super(JustMaskEm, self).__init__()
# 定义输入序列和标签序列
self.em_mask_one = paddle.nn.Embedding(voc_size, hidden_size)
self.em_mask_two = EmMask(voc_size, hidden_size, max_len)
self.head_layer = paddle.nn.Linear(hidden_size, voc_size,bias_attr=False)
self.layer_nor = paddle.nn.LayerNorm(hidden_size)
# 定义模型计算过程
def forward(self, x):
one = self.em_mask_one(x)
two = self.em_mask_two(x)
x = one* paddle.sum(two, -2).transpose([0,2,1])
# x = paddle.sum(x, -2)
# x=x.transpose([0, 2, 1])
# x = self.head_layer(self.layer_nor(x))
x = self.head_layer(self.layer_nor(x))
return x
def sample(self, x):
one = self.em_mask_one(x[:,-1:])
two = self.em_mask_two.sample(x)
x = one.squeeze(1)* two
# x = paddle.sum(x, -2)
# x=x.transpose([0, 2, 1])
# x = self.head_layer(self.layer_nor(x))
x = self.head_layer(self.layer_nor(x))
return x
# 进行模型训练和预测
if __name__ == '__main__':
net = JustMaskEm()
X = paddle.to_tensor([
[1, 2, 3, 4],
[5, 6, 7, 8]
], dtype='int64')
o=net(X)
t=net.sample(X)
print(net(X).shape)
print(net.sample(X).shape)
总结:
从上面实验数据可知 在使用方案 二的时候 ,如代码写 不断的扩大维度方可提高收敛时候的acc 上限且最高
且该网络模型可以在推理的时候如最后一幅图所示可以,进行单独解码 从而节约算力。
注意:
后面两幅图中 带框的两个是两个不同的方案,不带框的是公共部分
经过测试抛弃了蓝色框的方案。
更多推荐
 已为社区贡献13条内容
已为社区贡献13条内容






所有评论(0)