Dynamic Graph CNN for Learning on Point Clouds论文复现

本项目是我在参加『百度飞桨启航菁英计划』时关于论文Dynamic Graph CNN for Learning on Point Clouds的复现，这里主要是论文的主要内容介绍以及代码复现过程和结果的一些总结。我的复现代码是基于paddlepaddle-2.1.2写的，代码GitHub地址为: [https://github.com/JingfeiHuang/DGCNN_Paddle/tree/master](https://github.com/JingfeiHuang/DGCNN_Paddle/tree/master）

1. 论文解读

研究背景

从论文题目learning on point clouds可以看出，这篇论文主要是对点云做特征学习，提取的特征用于分类（shape-wise feature）、分割（point-wise feature）等。首先介绍一下什么是『点云』，简单来说就是一堆三维点的集合，必须包括各个点的三维坐标信息，其他信息比如各个点的法向量、颜色等均是可选。点云的文件格式可以有很多种，包括xyz，npy，ply，obj，off等（有些是mesh不过问题不大，因为mesh可以通过泊松采样等方式转化成点云）。对于单个点云，如果你使用np.loadtxt得到的实际上就是一个维度为（num_points,num_channels）的张量，num_channels一般为3，表示点云的三维坐标。一个可视化的例子如下图：

在点云特征学习方面影响力比较大的网络有PointNet，它直接对点云使用深度学习、解决了点云带来的一系列挑战，还有后续的PointNet++，本文类同PointNet++，基于ModelNet40做分类实验，然后还会有局部分割和场景分割的实验。
网络中的Graph CNN非常容易让人联想到GCN，但这篇论文不是直接用GCN对点云做表征学习，因为前面还有个dynamic，这个graph是动态建立的，这确实和GCN图结构建立后就一直固定不太一样。点云这种数据结构是离散的，缺乏拓扑信息（也就是单个点与点之间的关联并没有显式建立，但是他们之间应该是有实际意义的）。于是，如果能够通过某种方式建立点与点之间的拓扑关系，应该可以增强表征的能力，文中的EdgeConv的设计应运而生。

论文创新点

• 设计了EdgeConv，能够非常好地提取点云局部形状的特征，同时还能够保持排列不变性。
• 设计的DGCNN模型能够通过动态更新层与层之间的图结构来更好地学习点集的语义信息。
• EdgeConv具有普适性，可以很好地集成到多个已经存在的点云处理的pipeline中。
• 使用EdgeConv搭建的DGCNN网络，在多个基准数据集上取得了state-of-the-art的效果。

方法详解

网络结构

整体网络结构如下图所示，主要包括两个分支，分别用于分类和分割。主要思路是使用EdgeConv来表征，表征的方式是通过不断堆叠每一层EdgeConv的表征结果来进行的。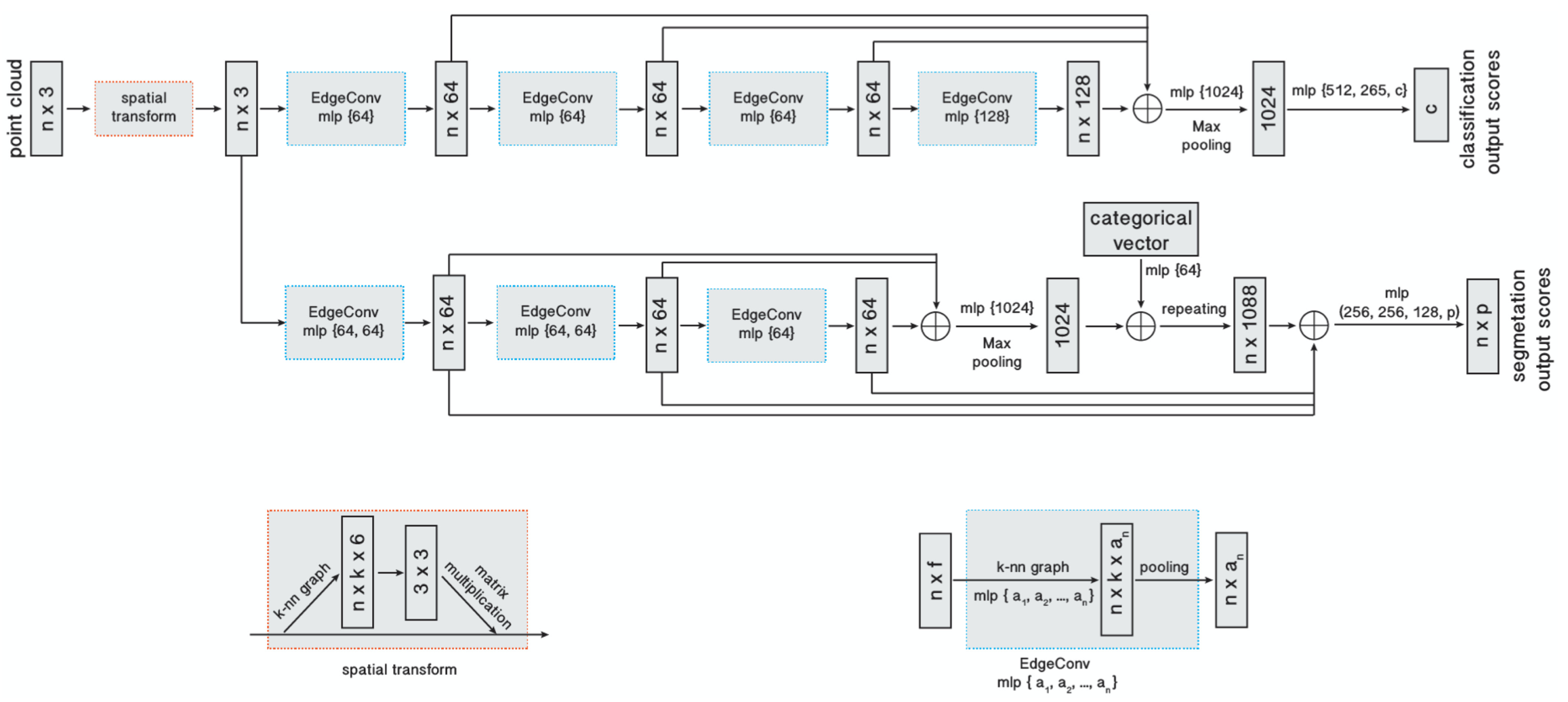

分类网络主要分为3步：

• 逐级对输入（包括坐标空间和特征空间）使用EdgeConv模块表征point-wise feature，也就是前一个EdgeConv模块的输出又为下一个EdgeConv模块的输入。
• 接着将不同层次的point-wise feature拼接起来，通过max pooling得到global feature。
• 最后接几个MLP用于分类，因为是ModelNet40数据集上40分类，因此最后输出维度是40。
  分割网络与分类网络基本类似，区别就是因为分割需要的是point-wise特征，因此分割网络在池化获得global feature之后需要repeat并与之前各个EdgeConv模块输出的point-wise feature相拼接，以此来获得全局特征和局部特征融合的point-wise feature（类似PointNet）。

EdgeConv

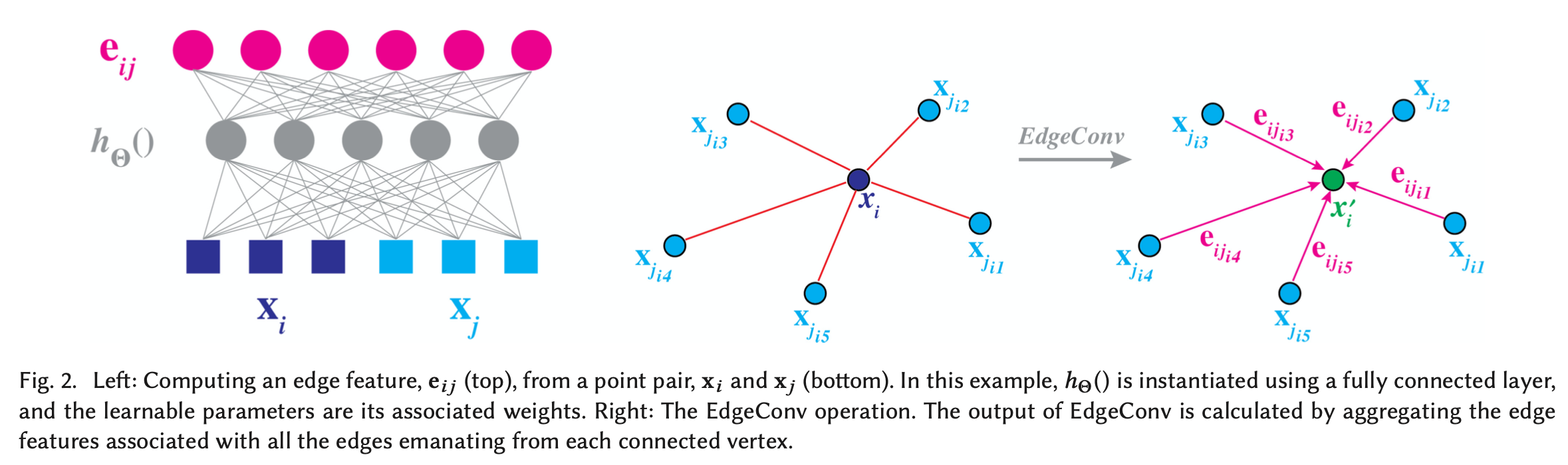
• 假设一个F维点云有n个点，定义为: $X=x_1,\dots ,x_n\in R^F$。最简单地情况下，F=3，即三维坐标。当然也可能包含额外的坐标，包含颜色、表面法线等等的信息。
• 在一个深度神经网络中，后面的层都会接受前一层的输出，因此更一般的情况下，维度F也可以表示某一层的特征维度。
• 假设给定一个有向图G=(ν,ϵ)，用来表示点云的局部结构，其中顶点为ν={1,…,n}，而边则为ϵ∈ν×ν。在最简单地情况下，我们建立一个KNN图G。假设距离点$x_i$最近的点$x_{j_{i1}},...,x_{j_{ik}}$包含许多有向边缘$(i,j_{i1}),...,(i,j_{ik})$。
• 我们定义边缘特征为$e_{ij}=h_{\Theta }(x_i,x_j)$，是一些使用一些可学习的参数$\Theta$构成的非线性函数。
• 最后在EdgeConv操作上添加一个通道级的对称聚合操作$\square$，完整公式为: ${x_i}^{\prime }={\square }_{j:(i,j)\in ϵ}{h}_{\Theta }(x_i,x_j)$
• 关于公式中的$h$和$\square$有四种可能的选择：
  a. $h_{\Theta }(x_i,x_j)={\theta }_j{x}_j$，聚合操作采用求和操作：${x_i}^{\prime }={\square }_{j:(i,j)\in ϵ}{\theta }_j{x}_j$
  b. $h_{\Theta }(x_i,x_j)=h_{\Theta }(x_i)$，只提取全局形状信息，而忽视了局部领域结构。这类网络实际上就是PointNet，因此PointNet中可以说使用了特殊的EdgeConv模块。
  c. $h_{\Theta }(x_i,x_j)=h_{\Theta }(x_j-x_i)$。这种方式只对局部信息进行编码，在本质上就是将原始点云看做一系列小块的集合，丢失了原始的全局形状结构信息。
  d. 第四种，也是文中采用的，$h_{\Theta }(x_i,x_j)=h_{\Theta }(x_i,x_j-x_i)$，这样的结构同时结合了全局形状信息以及局部领域信息。

图结构的动态更新

• 假设第$l$层的输出KaTeX parse error: Expected 'EOF', got '}' at position 24: …}^l,...,{x_n}^l}̲⊆R^{F_l}，而$X^0$就是输入点云。
• 实验表明，每次都重新计算每一层上的图中的点在特征空间中的最近邻点，是有用的。这也是动态图CNN与普通的图CNN的不同之处。
• 因此，将包含了这样的图的网络命名为动态图CNN（Dynamic Graph CNN, DGCNN）：
  a. 每一层都会得到一个不同的图$G^l=({\nu }^l,{ϵ}^l)$。
  b. 每一层的边缘特征为$(i,j_{i1}),...,(i,j_{ik})$，取决于点${x_i}^l$的$k_l$个最近邻的点$x_{j_{i1}},...,x_{j_{ik}}$。
  c. 更新公式：${x_i}^{l+1}={\square }_{j:(i,j)\in {ϵ}^l}{h_{\Theta }}^l({x_i}^l,{x_j}^l)$

与其他方法比较

• 主要跟两类方法做对比：一个是PointNet系列，一个是图CNN系列。
• PointNet是这个网络的一种特殊情况，即取KNN图的K=1，即图中的边都为空。PointNet中的边缘特征函数为$h(x_i,x_j)=h(x_i)$，仅仅考虑了全局几何信息而丢弃了局部信息。PointNet中的聚合操作$\square =max$（或者∑），其实就相当于全局最大池化（或平均池化）。
• PointNet++试着通过在局部区域使用PointNet来提取点云的局部结构信息。PointNet++的边缘特征函数也是$h(x_i,x_j)=h(x_i)$，聚合操作也是最大池化。
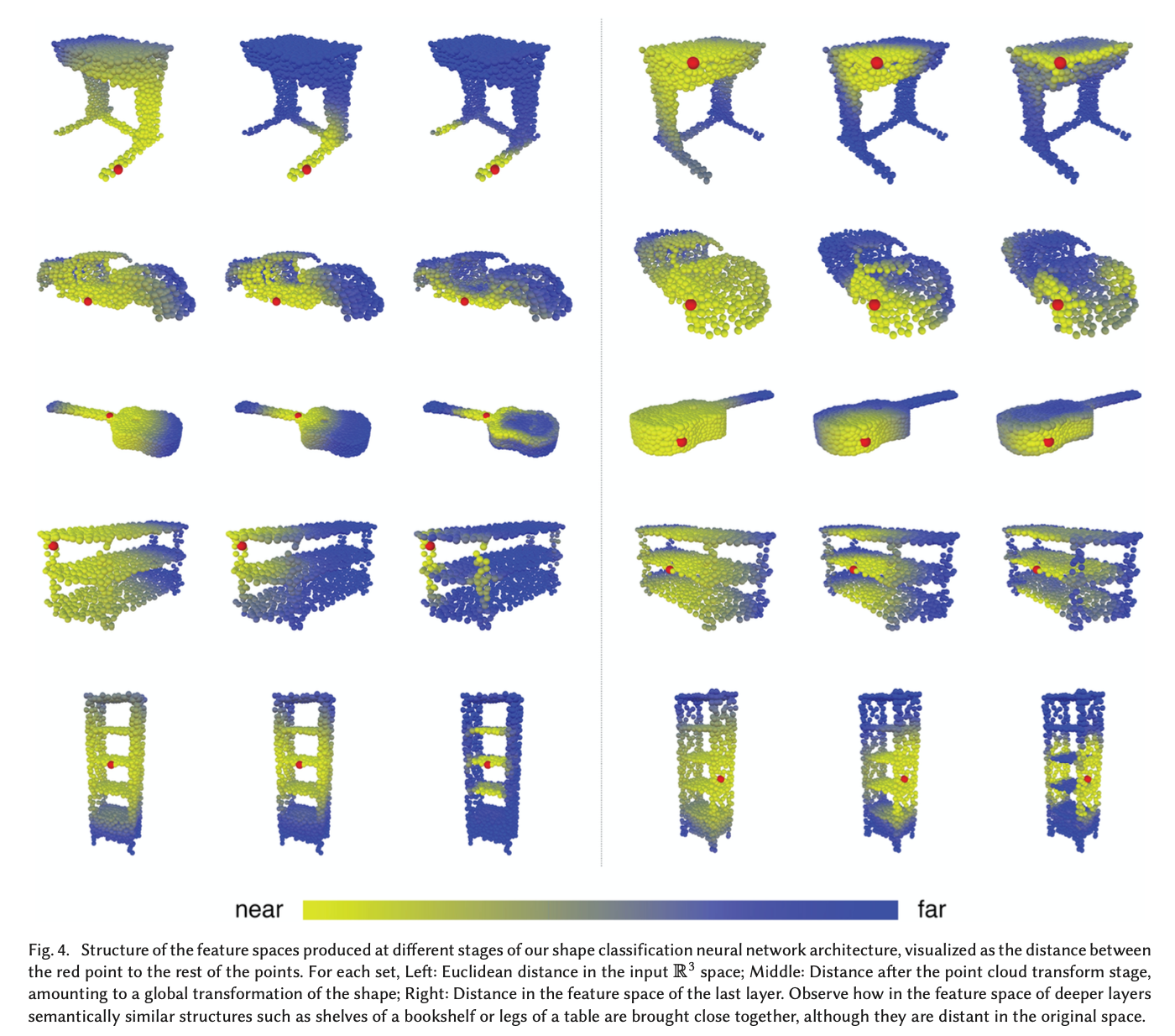
• 下图显示了不同特征空间的距离，证实了在更深层上的距离也能在长距离范围内携带语义信息。
  

实验结果

基于ModelNet40的分类实验结果如下图所示：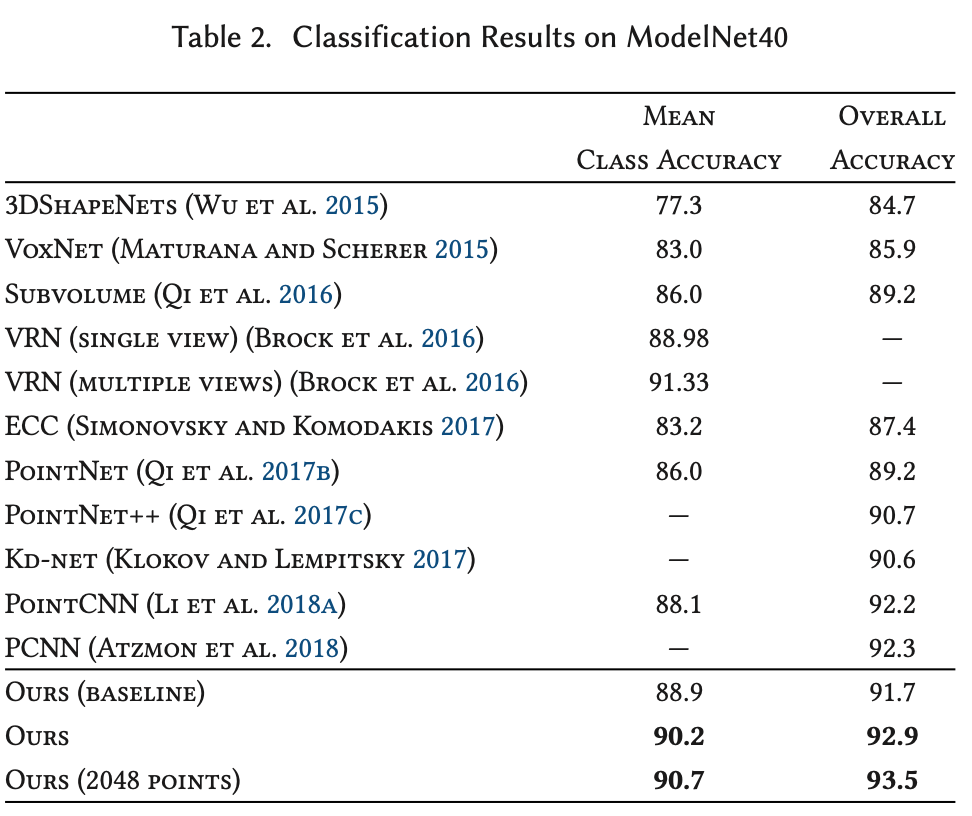

不同网络模型的复杂度、时间、准确率比较如下图所示：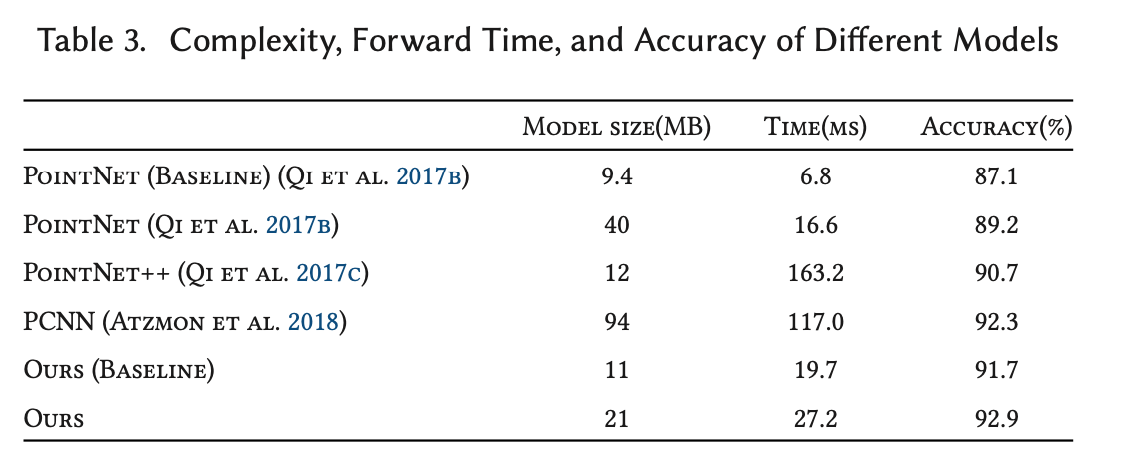

官方源码

github链接：https://github.com/WangYueFt/dgcnn

2. 复现过程介绍

准备数据集

实验中用到的数据集是ShapeNet，通过如下代码在线下载并解压到指定路径

def download():
    BASE_DIR = os.path.dirname(os.path.abspath(__file__))
    DATA_DIR = os.path.join(BASE_DIR, 'data')
    if not os.path.exists(DATA_DIR):
        os.mkdir(DATA_DIR)
    if not os.path.exists(os.path.join(DATA_DIR, 'modelnet40_ply_hdf5_2048')):
        www = 'https://shapenet.cs.stanford.edu/media/modelnet40_ply_hdf5_2048.zip'
        zipfile = os.path.basename(www)
        os.system('wget --no-check-certificate %s; unzip %s' % (www, zipfile))
        os.system('mv %s %s' % (zipfile[:-4], DATA_DIR))
        os.system('rm %s' % (zipfile))

网络结构部分代码

class DGCNN(nn.Layer):
    def __init__(self, args, output_channels=40):
        super(DGCNN, self).__init__()
        self.args = args
        self.k = args.k
        
        self.bn1 = nn.BatchNorm2D(64)
        self.bn2 = nn.BatchNorm2D(64)
        self.bn3 = nn.BatchNorm2D(128)
        self.bn4 = nn.BatchNorm2D(256)
        self.bn5 = nn.BatchNorm1D(args.emb_dims)

        self.conv1 = nn.Sequential(nn.Conv2D(6, 64, kernel_size=1, bias_attr=False),
                                   self.bn1,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv2 = nn.Sequential(nn.Conv2D(64*2, 64, kernel_size=1, bias_attr=False),
                                   self.bn2,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv3 = nn.Sequential(nn.Conv2D(64*2, 128, kernel_size=1, bias_attr=False),
                                   self.bn3,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv4 = nn.Sequential(nn.Conv2D(128*2, 256, kernel_size=1, bias_attr=False),
                                   self.bn4,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.conv5 = nn.Sequential(nn.Conv1D(512, args.emb_dims, kernel_size=1, bias_attr=False),
                                   self.bn5,
                                   nn.LeakyReLU(negative_slope=0.2))
        self.linear1 = nn.Linear(args.emb_dims*2, 512, bias_attr=False)
        self.bn6 = nn.BatchNorm1D(512)
        self.dp1 = nn.Dropout(p=args.dropout)
        self.linear2 = nn.Linear(512, 256)
        self.bn7 = nn.BatchNorm1D(256)
        self.dp2 = nn.Dropout(p=args.dropout)
        self.linear3 = nn.Linear(256, output_channels)

    def forward(self, x):
        batch_size = x.shape[0]
        x = get_graph_feature(x, k=self.k)
        x = self.conv1(x)
        x1 = x.max(axis=-1, keepdim=False)

        x = get_graph_feature(x1, k=self.k)
        x = self.conv2(x)
        x2 = x.max(axis=-1, keepdim=False)

        x = get_graph_feature(x2, k=self.k)
        x = self.conv3(x)
        x3 = x.max(axis=-1, keepdim=False)

        x = get_graph_feature(x3, k=self.k)
        x = self.conv4(x)
        x4 = x.max(axis=-1, keepdim=False)

        x = paddle.concat((x1, x2, x3, x4), axis=1)

        x = self.conv5(x)
        x1 = F.adaptive_max_pool1d(x, 1).reshape(shape=[batch_size, -1])
        x2 = F.adaptive_avg_pool1d(x, 1).reshape(shape=[batch_size, -1])
        x = paddle.concat((x1, x2), axis=1)

        x = F.leaky_relu(self.bn6(self.linear1(x)), negative_slope=0.2)
        x = self.dp1(x)
        x = F.leaky_relu(self.bn7(self.linear2(x)), negative_slope=0.2)
        x = self.dp2(x)
        x = self.linear3(x)
        return x

运行

训练

python main.py --exp_name=dgcnn_1024 --model=dgcnn --num_points=1024 --k=20 --use_sgd=True

python main.py --exp_name=dgcnn_2048 --model=dgcnn --num_points=2048 --k=40 --use_sgd=True

测试

python main.py --exp_name=dgcnn_1024_eval --model=dgcnn --num_points=1024 --k=20 --use_sgd=True --eval=True --model_path=checkpoints/dgcnn_1024/models/model.pdparams

python main.py --exp_name=dgcnn_2048_eval --model=dgcnn --num_points=2048 --k=40 --use_sgd=True --eval=True --model_path=checkpoints/dgcnn_2048/models/model.pdparams

复现结果

模型训练了98个epoch，相应测试结果如下图所示，分类准确率能达到源码的训练效果。