来源：PaperWeekly
本文约4500字，建议阅读10分钟
回顾经典电影，探究AI幻想有哪些走入我们的生活。

近三十年前，Sepp Hochreiter 与 Jürgen Schmidhuber 提出 LSTM，彻底改变了序列建模的走向。如今，Hochreiter 团队将目光投向大模型时代最关键的问题——Scaling Laws。

在 2024 年提出 xLSTM（Extended LSTM）架构之后，他们进一步展开了系统性的规模化研究，探讨这种线性时间复杂度的循环模型，能否在相同算力下与 Transformer 正面竞争：谁的损失更低，谁的推理更快，谁能在长上下文中保持稳定？

把记忆型架构放回同算力口径下比较后，「尺度」被更具体地落在成本—效果上。

论文标题：

xLSTM Scaling Laws: Competitive Performance with Linear Time-Complexity

论文链接：

https://arxiv.org/pdf/2510.02228

代码&数据集链接：

https://github.com/NX-AI/xlstm_scaling_laws

01 当“注意力”遇到“线性时间”

自注意力的两难

Transformer 靠全局注意力拿到了强表征，但代价很直白：prefill 对上下文长度 T 的开销近似二次增长；生成阶段里 KV/状态的带宽与容量成了吞吐上限。上下文从 2k 拉到 8k、16k，这笔“长度税”会按平方级往上跳。

xLSTM的取舍

xLSTM 并非“复古”，而是将序列混合交由 mLSTM 的递归动力学完成，使复杂度随 T 线性增长；其余模块遵循现代训练范式（更稳的归一化、更深的堆叠、配合前馈 MLP 与按维并行）。

分歧在混合方式：注意力 vs. 递归。由此在训练与推理两端，长上下文的边际成本更可控。

为什么从Scaling Laws入手？

今天的核心问题不是“用哪种模型”，而是“给定算力，怎样最省”。

为此，作者没有堆一串 benchmark，而是做了一套可复用的规模化实验学：两类架构（Transformer/xLSTM）、两种训练配置（IsoFLOP/Token-Param）、三档上下文长度，共 672 次训练，模型规模 80M→7B，预算 2.8×10^18→8.5×10^22 FLOPs，训练 token 2B→2T。

接着通过参数—数据—损失曲面 L(N,D) 与 IsoFLOP 等算力分析，量化“参数—数据—算力”的关系，便于在固定预算下讨论最优配比与可达边界。

在同算力的口径下，比较“谁更接近前沿”才有意义；具体对比与完整读图见实验结果第 1 节（Fig. 4）。

02 论文方法

下面进入具体做法。要回答“规模化到底值不值”，第一步是把代价和收益放到同一张坐标纸上：用模型参数规模 N 和训练 token 数 D 去解释验证损失的变化。先建立 L(N,D) 的统一表述，随后在等算力约束下讨论最优的规模与数据，再把推理延迟拆成计算与带宽两部分。

验证损失的参数–数据曲面 L(N,D)

作者将验证损失表示为模型规模 N 与训练 token 数 D 的函数，并用下式拟合整体趋势：

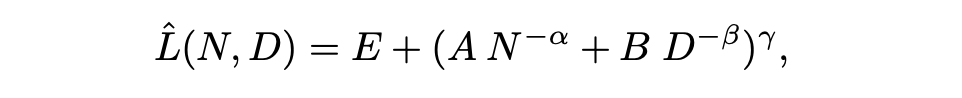
E 可看作“地板”；N 与 D 各自带来下降项；γ 刻画两条路径的耦合形态。好处是把“扩参/加数据”放到同一张曲面上，既能看最优附近，也能在“小模型＋大数据”的区域保持稳定判断。

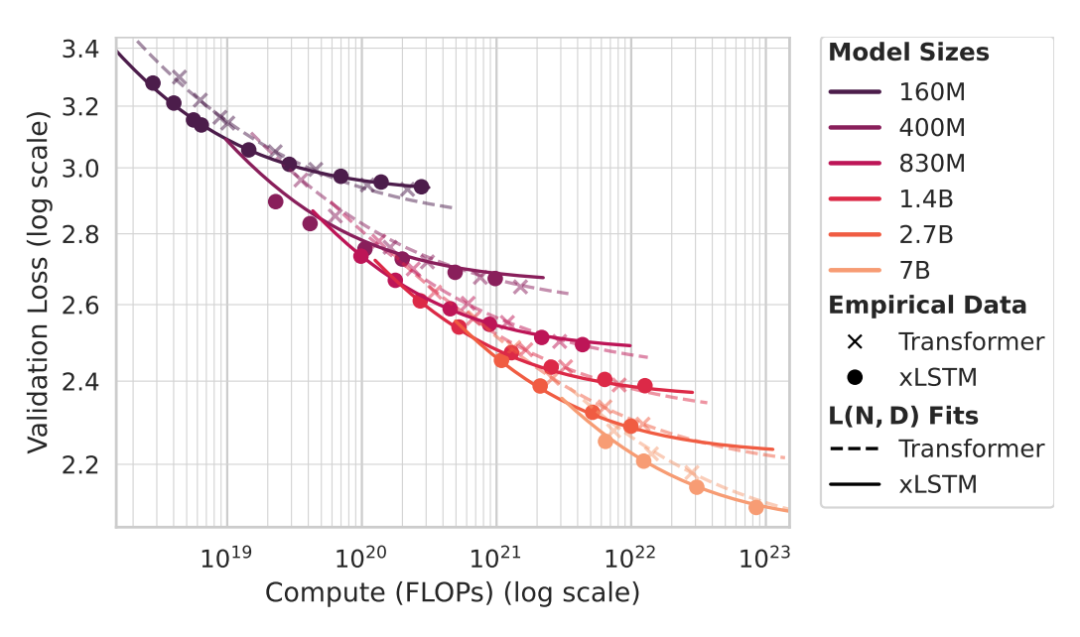
图1. 一张曲面看清扩参/加数据的边际收益

等算力约束下的最优规模与数据

算力预算记为 H。沿 C(N,D)=H 的等算力轨迹，先在每条轨迹上定位极小值，再将这些最优点跨预算拟合为幂律：

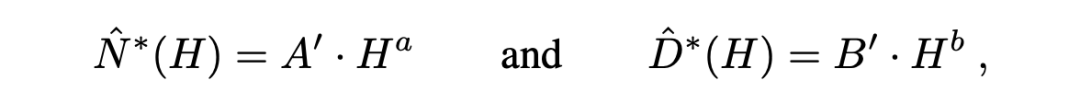
这两条“增长律”把“预算翻倍时，参数与数据各涨多少”写成明确规则，可据此推导预算—规模—数据的配比规则。

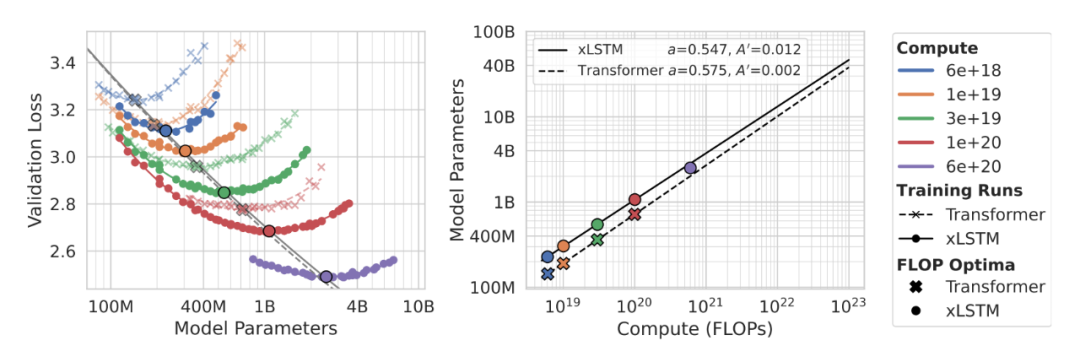
图2. 等算力下的最优规模如何随预算变化

推理时间的计算项与带宽项

推理阶段拆成两部分：prefill 近似 compute-bound，逐步生成近似 memory-bound。论文用下式拟合：

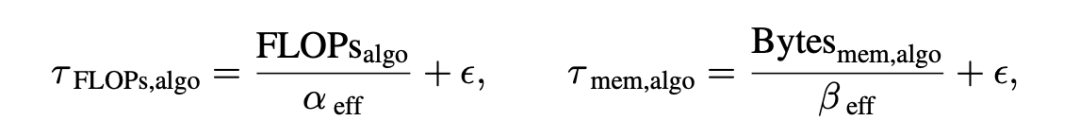
具体曲线与对比见实验结果·第 4 节（Fig. 6）。

03 实验结果

我们把对比拉回到“成本—效果”的坐标纸上来谈：在相同预算下谁更省、当模型较小但数据充足时是否依旧稳定、上下文拉长后最优规模会往哪里移动，以及推理阶段究竟受算力还是带宽所限。

与其盯着单点成绩，不如看这些趋势在多档预算、不同配置和长短上下文之间是否一致、可复现、可解释——只有这样，结论才具备工程可迁移性。

算力—损失前沿对比

在“预算—损失”平面上，横向看同 FLOPs 谁的损失更低，纵向看同损失谁的 FLOPs 更少。xLSTM 在较宽预算区间更靠近左下角，更接近帕累托前沿。

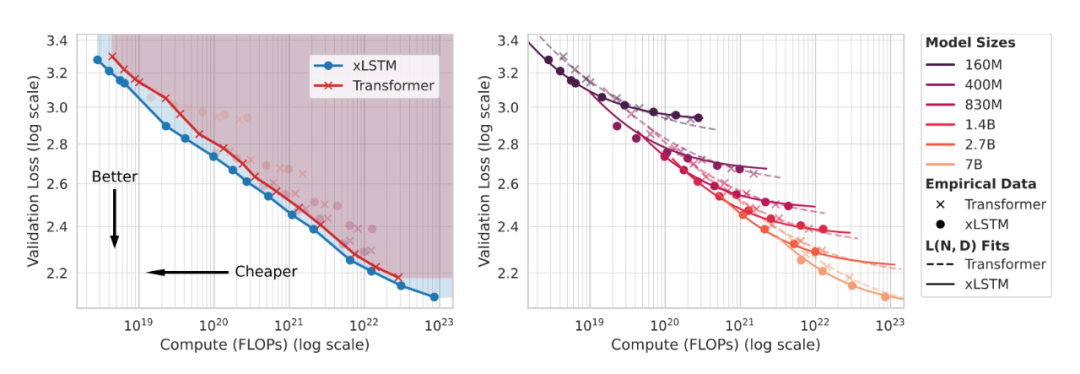
图3. 同预算看损失、同损失看预算，谁更接近前沿

此处我们应该关注“每个 FLOP 是否更值钱”，而不只是“谁堆得更高”。

过训练区的缩放稳定性

把 Token/Param 比拉到高档位，观察“小模型＋大数据”是否会“拐崩”。结果是：多档位上两类架构的“损失—预算”曲线近似平行下降，幂律指数稳定；差异主要在系数项。这意味着只要优化与数据工程到位，小而密可以长期吃到增益。

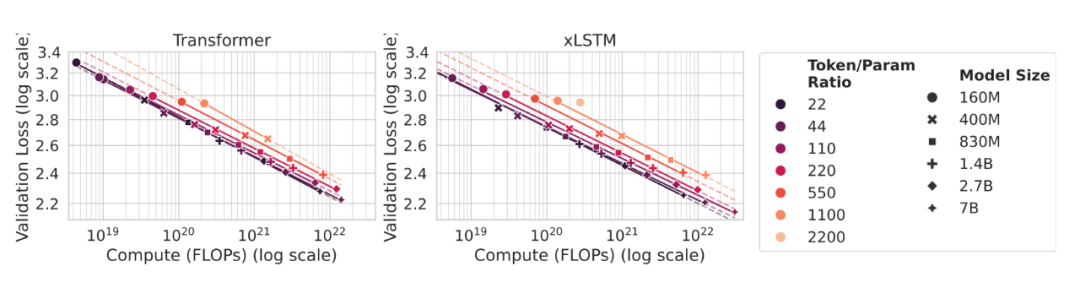
图4. 高token/param档位下仍保持平行幂律

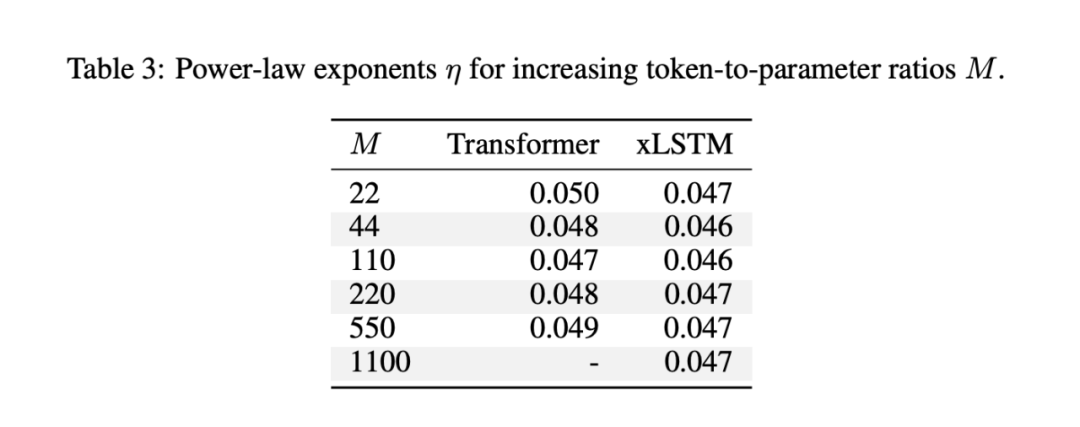
表1. 幂律指数在不同Token/Param档位的统计

上下文长度对最优规模的影响

上下文从 2k 拉到 8k、16k：注意力的二次项更快侵占预算，Transformer 的最优规模   下滑更明显；xLSTM 因线性时间的关系，下降更温和。这与两者的复杂度结构一致，并会同时影响训练成本与推理延迟。

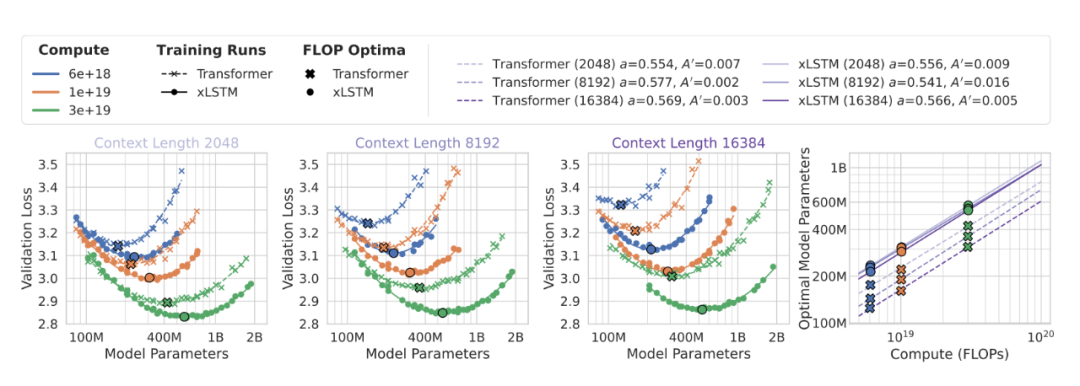
图5. 上下文越长，谁的最优规模更抗压

推理延迟与硬件视角

用式 (4) 定位瓶颈：prefill 端优先把   拉近硬件上限（编译、算子融合、批排）；生成端盯住 KV/状态的访存路径（压缩、分页、流水），提升   的有效利用。到 16k 上下文时，xLSTM 的 TTFT 与 step-time 优势清晰。

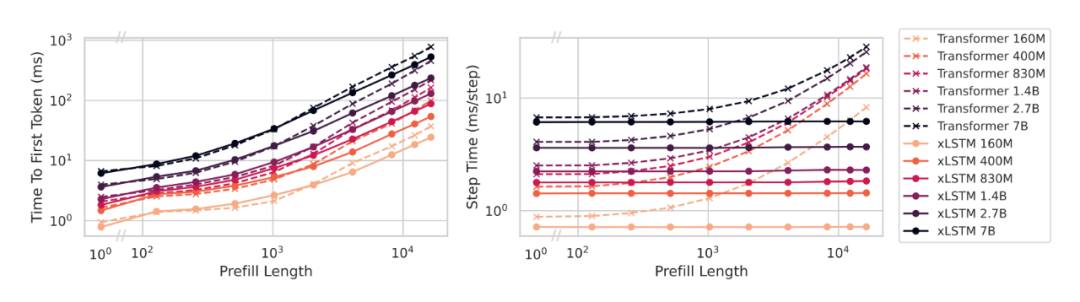
图6. 上下文拉长后，延迟曲线的差异

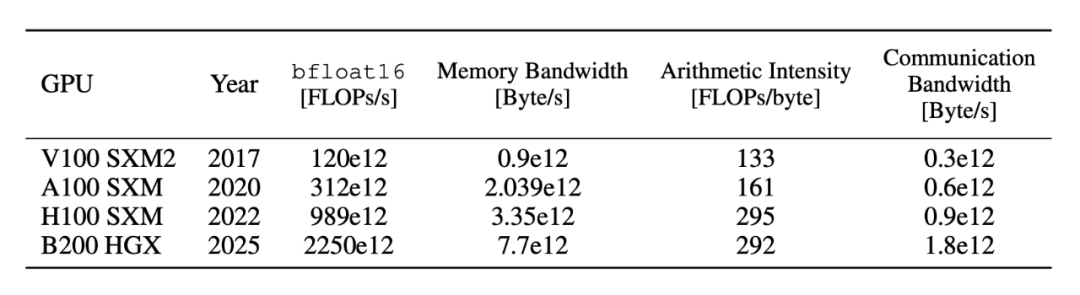
表2. 硬件“上限表”速览

图注：峰值 FLOPs、内存带宽、算术强度，帮助快速定位“算力项/带宽项”的上限与缺口。

04 当尺度成了主语，记忆路线重新入场

在我看来，这篇工作的关键不在“换个结构”，而在换了坐标系：用成本—效果的视角检验缩放规律。在线性时间的前提下，xLSTM 在等算力前沿、长上下文与推理曲线上的一致性，更像是规律层面的结论而非单点胜负。

这篇工作把“模型之争”从结构口味拉回到成本—效果的根坐标：在同样的训练算力下，谁更接近前沿；在长上下文里，谁的曲线更平缓；在过训练区，谁的缩放更稳定。

作者并没有用新的花哨模块来取胜，而是用三件可核对的工具把尺度问题说清楚：一张   的损失曲面，回答“扩参/加数据是否还值”；一对等算力下的最优幂律，回答“预算翻倍该往哪里加”；一个把推理拆为“算力项＋带宽项”的时间模型，回答“延迟曲线为什么这样”。

在这套坐标里，在线性时间的前提下，xLSTM 在等算力前沿、长上下文与推理时延上呈现出一致的趋势性优势；这更像是缩放规律层面的结果，而不是单点榜单的起伏。

更有意思的是，“过训练区的平行幂律”把一个常被误解的问题澄清了：当 Token/Param 比很高时，曲线并未失真，指数仍然稳定，差别主要落在系数。这意味着“把数据当作第一资源”的做法并不是某个阶段的权宜之计，而是一条可以被定量描述、可复现的缩放路径。

与此同时，上下文长度被纳入了一等变量的地位：当   增长，注意力的二次项会直接改写预算的可用形状，最优规模随之下滑；线性时间的记忆架构则把算力留给真正提升表达力的部分。这不是“情怀式复古”，而是把记忆动力学与现代训练范式在尺度层面上重新拼接。

当然，论文也给出了边界。  的曲面拟合在最优附近与常见过训练区内表现稳健，但跨分布迁移或走到极端配置时仍需重新校准；推理端的  、  带有系统与硬件的印记，不能把系统差异误读成架构差异；而“前沿更近”并不自动等于“任务全面更强”，把验证损失与下游表现打通仍是后续工作。

换句话说，这篇文章给出的是尺度—成本意义上的强证据链，而不是所有维度的终局判断。

把这些线索合起来看，Hochreiter 团队的贡献并不在于给出一个“新的万能架构”，而在于调整了观察问题的主语：当我们把预算、长度与时间拆开看，线性时间的记忆模型就不再是“过去的技术”，而成为一种在特定资源与需求组合下可证明更划算的选择。

今天的大模型讨论里，争论常常停留在“注意力是否万能”的层面；这篇论文提醒我们，尺度才是主语。在这个主语之下，xLSTM 展现出的那条更线性的曲线，至少为“注意力之外的路径”提供了严肃、可复现的证据。

编辑：王菁

关于我们

数据派THU作为数据科学类公众号，背靠清华大学大数据研究中心，分享前沿数据科学与大数据技术创新研究动态、持续传播数据科学知识，努力建设数据人才聚集平台、打造中国大数据最强集团军。

新浪微博：@数据派THU

微信视频号：数据派THU

今日头条：数据派THU