【强化学习】信任区域策略优化(Trust Region Policy Optimization,TRPO)
摘要:本文介绍了信任区域策略优化(TRPO)算法,针对策略梯度法(PG)存在的数据利用率低、更新幅度不可控等问题进行了改进。TRPO通过引入信任区域概念,在优化目标中加入KL散度约束,确保新策略不会偏离旧策略太远。其核心在于使用重要性采样修正策略分布偏差,允许对同一批数据进行多次小批量更新,提高样本利用率。相比PG,TRPO能实现更稳定的策略优化和性能提升,为后续PPO算法的提出奠定了基础。
本文要介绍的是信任区域策略优化(Trust Region Policy Optimization,TRPO算法,在正文开始之前,可参考我的 强化学习专栏 复习强化策略梯度方法,REINFORCE算法,蒙特卡洛方法等概念 ^ _ ^
策略梯度方法的问题
之前我们介绍过策略梯度法(PG),但它存在以下问题:
-
学习率的选择: 策略参数进行梯度更新来提升策略: θ t + 1 = θ t + α ∇ θ J ( θ ) \theta_{t+1} = \theta_{t} + \alpha \nabla_{\theta} J(\theta) θt+1=θt+α∇θJ(θ) ,如果学习率选择过大,会导致策略的更新幅度过大,使得策略性能急剧下降,甚至直接崩溃;如果选择过小,会导致策略的更新速度过慢,训练效率低下。
-
数据无法复用:
普通策略梯度 (PG) 的流程如下:
- 用当前策略 π θ 0 \pi_{\theta_0} πθ0 采样数据 s 0 s_0 s0;
- 用采样数据计算策略梯度,更新一次策略参数 ,得到新策略 π θ 1 \pi_{\theta_1} πθ1;
- 更新后策略已经变了,那么之前由策略 π θ 0 \pi_{\theta_0} πθ0 采样得到的数据 s 0 s_0 s0不再符合新策略 π θ 1 \pi_{\theta_1} πθ1的分布,所以无法再用那批数据继续更新策略
- 重新采样,继续以上操作,继续更新策略
PG 是「采样数据→ 立刻更新 → 数据废弃」的,一批数据只能用一次,更新后数据分布变了,旧数据就不再符合当前策略分布了
-
更新无约束:策略更新幅度无约束,新旧策略的分布差异可能过大,导致基于旧策略采样的数据无法有效指导新策略学习,样本利用率低
-
样本方差大: 策略梯度优化一个核心的假设是可以通过采样的方法来估计策略的梯度。但是当问题的规模变得非常大:比如每次轨迹都非常长,又或者策略模型非常大,为了预估准确的梯度,我们就不得不采样多次,否则就会面临方差很高的问题。
信任区域策略优化(Trust Region Policy Optimization,TRPO和 近端策略优化(Proximal Policy Optimization,PPO是对PG的改进,它们通过引入约束或者限制,来确保每次策略的更新不会太大,从而避免策略崩溃,同时又能够保证策略的持续提升。本文主要介绍TRPO。
TRPO
信任区域策略优化(Trust Region Policy Optimization,TRPO)的核心思想是引入信任区域 的概念。所谓信任区域,指的是在这个区域内,我们可以信任当前的策略梯度,进行策略的更新。当策略更新超出这个信任区域时,我们就需要重新评估策略的性能,并调整更新方向。
TRPO的优化目标函数是:
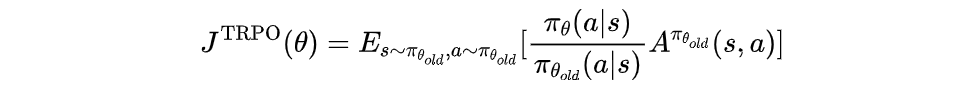
其中, π θ o l d \pi_{\theta_{old}} πθold是旧策略, π θ \pi_{\theta} πθ是新策略, A π θ o l d A^{\pi_{\theta_{old}}} Aπθold是优势函数。这个目标函数和普通的策略梯度方法类似,都是希望最大化期望的累积回报。但将累积奖励 G ( τ ) = ∑ t = 0 T γ t r t G(\tau)=\sum_{t=0}^T \gamma^t r_t G(τ)=∑t=0Tγtrt 改为了优势函数 A π θ o l d A^{\pi_{\theta_{old}}} Aπθold,轨迹是从旧策略 π θ o l d \pi_{\theta_{old}} πθold中采样的,目标函数还在优势函数上加了重要性权重 π θ π θ o l d \frac{\pi_\theta}{\pi_{\theta_{old}}} πθoldπθ ,用于修正更新后的策略分布和旧策略上采样的数据分布的偏差。
TRPO与普通策略梯度方法的区别在于,它引入了一个约束条件,保证新策略与旧策略的差距不能太大:
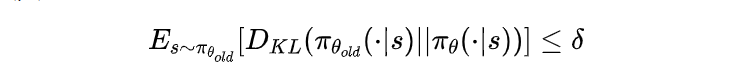
其中, D K L D_{KL} DKL是KL散度,用来衡量两个策略之间的差异; 是一个预先设定的超参数,表示信任区域的大小。这个约束条件确保了新策略不会偏离旧策略太远,从而保证了策略的单调提升。
TRPO的算法流程:
- 采样: 用当前策略 π θ 0 \pi_{\theta_0} πθ0 采数据,把它冻结,命名为 π θ o l d \pi_{\theta_{old}} πθold ,表示旧策略
- 计算优势函数: 使用GAE或其他方法计算每一步的优势函数值 A π θ o l d ( s , a ) A^{\pi_{\theta_{old}}}(s,a) Aπθold(s,a)。
- 构建目标函数和约束条件: 根据上述公式构建TRPO的目标函数和约束条件。
- 求解优化问题: 解带约束的优化问题,得到策略更新量 δ θ \delta \theta δθ。
- 更新策略: 使用得到的策略更新量更新策略参数: θ n e w = θ o l d + δ θ \theta_{new} = \theta_{old} +\delta \theta θnew=θold+δθ。
- 迭代: 使用更新后的策略作为新的旧策略,重复上述步骤。
PPO对TRPO进行了优化(下章介绍),他们都有两个策略,一个是旧策略,一个是新策略,先对于普通策略梯度 (PG) 的始终一个策略,他们的区别在哪?
普通策略梯度方法中,每个数据样本只进行一次梯度更新,而TRPO和PPO可以对同一批采样数据进行多个 epoch 的小批量更新 ,可以提高样本复用率,同一批数据可以被充分利用,每次只更新小步(小批量),可以平稳优化策略,每次更新幅度小,使得新策略不会偏离旧策略太远。为了让TRPO和PPO在同一批旧策略数据上可以进行多个 epoch 的小批量更新(想用旧策略采样数据来估计新策略的期望回报),TRPO和PPO就是用了重要性采样的思想,通过重要性权重 π θ π θ o l d \frac{\pi_\theta}{\pi_{\theta_{old}}} πθoldπθ 修正更新后的策略分布和旧策略上采样得到的数据分布的偏差。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)